The output units Oi are arranged in an array and are fully connected to the inputs with arc weight wij.
A competitive learning rule is used, choosing the output unit with weight vector, wi*, closest to the current input I:
- ||wi*-I|| <= ||wi - I||,
for all i
The neuron update function is critical for topology preserving networks.
The update function is defined in terms of a
neighbourhood function 
equals to 1 for i=i*,
the winning neuron, and falls off rapidly when neurons get far from it in the output array.
Units close to the winner, as the winner itself, should
have their weights changed
appreciably, while those further away (where is small)
should have little effect. A typical choice for is:
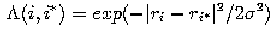
where sigma is a width parameter that is gradually decreased.
- Step 1
Initialization: select the size and structure of the network. Initialize wij with small random values. - Step 2
Present a new input I(tk) in the N-dimensional real set.- Step 3
Compute the distance between I(tk) to all neurons, or the matching scores di's:
di= || I(tk)-wi(tk)||,
where ||*|| is the Euclidean norm or the infinity norm or any norm p.- Step 4
Select the i*th neuron closest to I(tk), or minimum distance di*:
di*=min(di).- Step 5
Update weight vectors to the i*th neuron and its neighbours.
where eta is usually a slowly decreasing function of time and eta is great than 0 and less of 1.- Step 6
Repeat from step 2. - Step 3
This figures shows an example of net, mapping 2 inputs I1 and I2 onto a 10x10 planar array. Input pattern were chosen randomly from a triangular uniform distribution which is shown as the triangle in the Edit and Simulation Window. The weights (wi1, wi2 ) for each output unit are shown in this input space by an intersection in the grid of lines, which connects all nearest neighbour pairs.
Another example: 3 different times during the process of learning a rectangular shape, with a net of 2 input neuron connecting 199 neurons laying on a line.
Back to index
