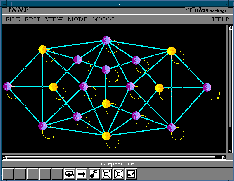
Figure 2: The Boltzmann machine module and control panel with options menu
Simulation of Back-error propagation
INNE: a Neural Network
INNE architecture
The first neural model available in INNE is the Boltzmann machine, a combinatoric optimization model implementing the probabilistic optimization algorithm called simulated annealing [Her91] and able to avoid local optimal solutions (i.e. networks that do not change dynamically their structure). In the module, a learning algorithm for classification problems is implemented as well, even though the back-error propagation learning algorithm is more efficient to this purpose. The Boltzmann machine can be used to solve combinatorial problems by approximation [AHS85]; this can be shown by loading the network of Fig. 2 that solve the Indipendent set problem. The objective is to find the greatest number of independent nodes not connected directly with each other on undirected graphs.
Users can choose between deterministic or stochastic behaviour and select the sequential, random or full parallel mode of updating the network and experiment the speed of reaching a stable state. The machine can be trapped into local optimal configurations. The experiment will show that the random parallelism mode can be very effective in the stochastic behaviour even though no convergence theorem has been proved so far. In the deterministic case the Boltzmann machine is a Hopfield model which offers the best computational time in the sequential mode as it reaches immediately a stable state choosen at random among local optimal configurations.
Simulation of Back-error propagation
INNE: a Neural Network
INNE architecture