Geobject - Tutorial

Handbook - Tutorial - Problems about circumferences

Build the tangents to a circumference in a given point not on the circumference itself

Let A be the center of a circumference (built using Circle) and C a point external to it.
We have to draw the lines tangent to the circumference passing through the point C.
Build the segment CA, using Segment with two points.
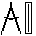Build a circumference centered in the middlepoint of the segment and having the segment as diameter, using Circle with center point.
This circle intersects the given one in H and G.
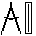Build two lines, CH and CG, using Line.
They are the tangents desired. Infact, should you joined A with H and G, the angles AHC, AGC, enscribed in a halfcircumference, would be rect. That's why the lines CH and CG are perpendicular to the rispective radius AH, AG and so they are tangent to the circumference in H, G.