

Next: Statistical tests to assess
Up: Background on stability based
Previous: Stability based methods
Stability indices
Let be  a clustering algorithm,
a clustering algorithm, 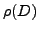 a given random perturbation procedure applied to a data set
a given random perturbation procedure applied to a data set 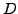 and
and 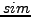 a
suitable similarity measure between two clusterings (e.g. the Fowlkes and Mallows similarity [13]).
For instance
a
suitable similarity measure between two clusterings (e.g. the Fowlkes and Mallows similarity [13]).
For instance 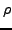 may be a random projection from a high dimensional to a low dimensional subspace [1], or a bootstrap
procedure to sample a random subset of data from the original data set
may be a random projection from a high dimensional to a low dimensional subspace [1], or a bootstrap
procedure to sample a random subset of data from the original data set 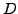 [4].
[4].
We define
 as the random variable given by the similarity between two k-clusterings obtained by applying a
clustering algorithm
as the random variable given by the similarity between two k-clusterings obtained by applying a
clustering algorithm  to pairs
to pairs 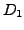 and
and  of random independently perturbed data.
The intuitive idea is that if
of random independently perturbed data.
The intuitive idea is that if 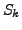 is concentrated close to
is concentrated close to 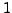 , the corresponding clustering is stable with respect to a given
controlled perturbation and hence it is reliable.
, the corresponding clustering is stable with respect to a given
controlled perturbation and hence it is reliable.
Let be 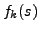 its density function, and
its density function, and
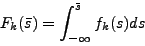 |
(1) |
its cumulative distribution function.
We define 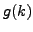 as the integral of the cumulative distribution function:
as the integral of the cumulative distribution function:
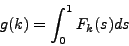 |
(2) |
Intuitively 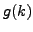 represents the "concentration" of the similarity values close to 1; that is, if
represents the "concentration" of the similarity values close to 1; that is, if 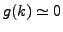 then
the distribution of the values of
then
the distribution of the values of 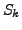 is concentrated near 1, or, in other words, the k-clustering is stable. On the
other hand, if
is concentrated near 1, or, in other words, the k-clustering is stable. On the
other hand, if 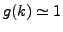 then the clusterings are totally unstable, while if the distribution is close to the
uniform distribution, we have
then the clusterings are totally unstable, while if the distribution is close to the
uniform distribution, we have
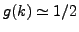 .
.
We may directly estimate eq. 2 by numerical integration, or we may more easily obtain 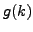 from the estimate of
the expectation
from the estimate of
the expectation ![$E[S_k]$](img20.gif) :
:
Hence from eq. 3 we may easily compute 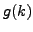 :
:
![\begin{displaymath}
g(k) = \int_0^1 F_k(s) ds = 1 - E[S_k]
\end{displaymath}](img25.gif) |
(4) |
Eq. 4 shows also more clearly that we have a very stable and reliable clustering (![$E[S_k]$](img20.gif) close to 1),
if and only if
close to 1),
if and only if 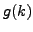 is close to 0.
is close to 0.


Next: Statistical tests to assess
Up: Background on stability based
Previous: Stability based methods
![]() as the random variable given by the similarity between two k-clusterings obtained by applying a
clustering algorithm
as the random variable given by the similarity between two k-clusterings obtained by applying a
clustering algorithm ![]() to pairs
to pairs ![]() and
and ![]() of random independently perturbed data.
The intuitive idea is that if
of random independently perturbed data.
The intuitive idea is that if ![]() is concentrated close to
is concentrated close to ![]() , the corresponding clustering is stable with respect to a given
controlled perturbation and hence it is reliable.
, the corresponding clustering is stable with respect to a given
controlled perturbation and hence it is reliable.
![]() its density function, and
its density function, and
![]() as the integral of the cumulative distribution function:
as the integral of the cumulative distribution function:
![]() from the estimate of
the expectation
from the estimate of
the expectation ![]() :
:
![]() :
: