Compactness of EP circuits

We aim to show that, for a significant class of functions, the representation through EP circuit is more compact than the corresponding Boolean circuit representation.

To this aim we need to introduce the following definitions.

Definition 1 (Total influence)   The total influence [5] of a Boolean function $\varphi$ is the sum of the individual influences of its variables

$$I(\varphi)=\sum_{j=1}^{r}I_j(\varphi)$$

Definition 2   For an odd integer $r$, the majority function $M(r)=M(z_1,\dots,z_r)$ equals $1$ if and only if $z_1+\dots+z_r> r/2$.

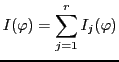
Alon-Boppana's theorem [2] affirms that, if a Boolean function $\varphi$ is expressed by a $d$-level circuit composed by the connectives AND-OR with size $N$, then

$$I(\varphi)\leq C_1 \log^{d-1}N$$ (6)

where $C_1$ is a suitable constant. Thus, for $2$-levels circuits the following inequality holds:

$$I(\varphi)\leq C_1 \log N$$ (7)

Consequently, since it can be simply verified that $I(M(r)) \simeq \sqrt{r}$, we obtain that, for the class of the majority functions

$$N \geq e^{\sqrt{r}}$$

and, then, that the size of a $2$-level circuit that represents a majority function increases exponentially with the number of its variables.

On the contrary, a majority function $M$ with $r$ entries can be represented by using an EP circuit with size $1$, independently from $r$. As a matter of fact, for representing $M(r)$ it is sufficient to use a single ES composed by all the $r$ variables with $q_1=(r+1)/2$. Thus, we obtain the following expression for $M(r)$

$$M(r)=[(z_1,\dots,z_r)_{(r+1)/2}]_1$$

leading to an EP circuit with size $1$. We can conclude that EP representation is more compact w.r.t. to the corresponding positive Boolean circuit representation.