Il termine "algoritmo"
- è sinonimo di "programma"
- designa una procedura che esegue una sequenza finita di operazioni
- designa una procedura che non termina necessariamente
- indica una formula di calcolo
L’algoritmo di ordinamento per inserimento (insertion sort)
- è particolarmente veloce quando l’array è quasi ordinato
- è particolarmente lento quando l’array è quasi ordinato
- ha prestazioni indipendenti dall’ordine
- ha complessità quadratica nel caso migliore
- è particolarmente veloce quando l’array è quasi ordinato
La somma di tutti gli interi compresi tra 1 e n
- vale
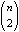
- vale
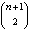
- vale (n^2)/2
- è un numero di Fibonacci
- vale
* La somma degli inversi dei primi n interi positivi, per n tendente a infinito,
- tende a una costante.
- diverge come log n.
- diverge molto rapidamente.
- non è né convergente né divergente.
* Un generatore pseudo-casuale lineare congruente
- fornisce numeri realmente casuali
- fornisce una lista lineare
- fornisce una sequenza periodica
- fornisce infiniti valori tutti differenti
Qualche calcolo! La relazione di ricorrenza f(n) = f(n – 1) + 2 f(n – 2) con f(0) = f(1) = 1 fornisce come valore di f(5)
- 8
- 21
- 43
- non si può calcolare f(5) se non viene specificato il valore di f(2)
* Un ladro cerca di aprire una cassaforte che ha un milione di possibili combinazioni numeriche. La sua particolare tecnica gli consente di stabilire se la combinazione che sta provando precede o segue, nell'ordine numerico, quella corretta. Per aprire la cassaforte avrà bisogno di provare al più circa
- un milione di combinazioni
- mezzo milione di combinazioni
- 100 combinazioni
- 20 combinazioni
I numeri di Fibonacci crescono in maniera
- lineare
- quadratica
- esponenziale
- doppiamente esponenziale
Un albero libero può essere definito come
- un grafo aciclico
- un grafo connesso
- un grafo non orientato, connesso e aciclico
- un grafo orientato aciclico
- un grafo aciclico
* Un albero binario con n nodi aventi 2 figli
- ha altezza log n
- ha altezza √n
- ha n + 1 nodi senza figli (foglie o nodi esterni)
- è completo
- ha altezza log n
Uno heap
- è un albero binario di ricerca
- è un albero binario completo in cui ogni nodo (tranne la radice) ha chiave non maggiore del padre
- è un albero binario in cui tutti i percorsi dalla radice alle foglie hanno esattamente la stessa lunghezza
- è un array in cui ogni elemento è non minore del successivo
Uno heap
- può essere gestito con un array
- è un albero binario in cui ogni nodo è maggiore del figlio sinistro e minore del destro
- ha la proprietà LIFO (Last In First Out)
- richiede necessariamente due puntatori per ogni nodo
HeapSort è asintoticamente ottimo?
- No, perché QuickSort è più veloce.
- No, perché non esistono algoritmi ottimi.
- Sì, perché ha complessità
Theta(n lg n) nel caso migliore. - Sì, perché ha complessità
O(n lg n) nel caso peggiore.
Uno heap con n elementi
- può essere costruito in tempo logaritmico
- può essere costruito in tempo lineare
- richiede tempo Theta(n log n) per la costruzione
- richiede tempo almeno quadratico per la costruzione
Una coda a priorità
- non è altro che uno stack
- richiede necessariamente una lista
- ha la proprietà FIFO (First In First Out)
- può essere realizzata con uno heap
- non è altro che uno stack
E’ corretto dire che la complessità in tempo di Quicksort è O(n^2)?
- sì, perché O fornisce un estremo superiore
- no, perché la complessità nel caso medio è O(n log n)
- no, perché la complessità è
O(n log n) - occorre valutare diversi casi
- sì, perché O fornisce un estremo superiore
Per Quicksort
- il caso peggiore è comunque quadratico
- la versione randomizzata ha complessità O(n log n) anche nel caso peggiore
- la complessità è lineare se i dati sono ordinati
- il caso medio ha complessità quadratica
Per gestire la ricorsione in quicksort
- basta una pila di dimensione lg n.
- occorre una pila di dimensione n.
- occorre una pila di dimensione n^2.
- basta l'array di input e una quantità costante di memoria aggiuntiva.
- basta una pila di dimensione lg n.
Quale delle seguenti affermazioni è vera?
- non esistono algoritmi di ordinamento in tempo lineare
- non esistono algoritmi di ordinamento in tempo O(n log n) nel caso peggiore
- ogni algoritmo di ordinamento richiede almeno tempo O(n log n)
- non esistono algoritmi di ordinamento con tempo inferiore a O(n)
- non esistono algoritmi di ordinamento in tempo lineare
Tutti gli algoritmi di ordinamento basati sui confronti
- sono asintoticamente ottimi.
- hanno complessità
Omega(n lg n) nel caso peggiore. - hanno complessità
O(n lg n) nel caso peggiore. - hanno complessità
O(n^2) nel caso peggiore.
L'ordinamento per conteggio (counting sort) ordina in tempo lineare
- sempre e comunque.
- se il file è già ordinato.
- se il valore k della chiave massima da ordinare cresce al più come n, ossia k=O(n).
- solo se le chiavi sono in numero finito.
Radix sort ordina in tempo lineare
- se il valore k della chiave massima da ordinare cresce al più come n, ossia k=O(n).
- se la lunghezza delle chiavi da ordinare resta costante al crescere di n.
- se si procede da destra a sinistra.
- se si usa counting sort per ordinare le cifre.
L'ordinamento "a secchi" (bucket sort) ordina in tempo lineare
- anche nel caso peggiore, se le chiavi sono ben distribuite.
- in media.
- solo se si crea un numero di secchi dell'ordine di n.
- ma non si può usare se le chiavi non sono nell'intervallo [0, 1).
La determinazione del massimo in un file di n elementi
- richiede n - 1 confronti.
- richiede Theta(n^2) confronti.
- richiede l'ordinamento del file.
- richiede lo stesso numero di confronti che per determinare simultaneamente massimo e minimo.
La determinazione di una qualsiasi statistica d'ordine
- richiede l'ordinamento del file.
- può essere ottenuta in tempo lineare.
- può essere ottenuta in tempo lineare soltanto in media, perché il caso peggiore è quadratico.
- richiede il corso di CPSM, che non ho ancora seguito.
La struttura di dati "pila" (o "stack")
- può essere realizzata facilmente con un array.
- realizza una politica FIFO.
- serve per gestire le chiamate non ricorsive.
- realizza un heap.
L'uso di sentinelle
- è altrettanto pericoloso quanto l'uso del costrutto "go to".
- appesantisce inutilmente il codice.
- è utile per semplificare la gestione dei casi limite.
- rende più sicuro il codice.
La ricerca in una lista
- richiede in ogni caso tempo lineare
- richiede in ogni caso tempo costante
- richiede in media tempo logaritmico
- richiede in media tempo lineare
Per rappresentare alberi in cui ogni nodo ha un numero arbitrario di figli
- si possono usare opportuni alberi binari
- non si possono usare alberi binari
- occorre usare i B-alberi
- si possono usare solo le liste di adiacenza
Le tecniche hash
- richiedono grandi quantità di memoria
- hanno prestazioni che dipendono dal rapporto tra numero di scambi e numero di confronti
- hanno prestazioni che dipendono dal rapporto tra numero delle posizioni occupate e numero delle posizioni disponibili
- hanno prestazioni che dipendono solo dalla quantità di memoria allocata
L'indirizzamento aperto (open addressing)
- è una tecnica di gestione della RAM
- è una tecnica di gestione delle tabelle hash
- è una tecnica di scansione delle liste
- indica che un indirizzo di memoria contiene un indirizzo
Una ricerca senza successo in una tabella hash a indirizzamento aperto richiede in media 1/(1 - alfa) confronti, con alfa=n/m.
- E' vero, nell'ipotesi di uniformità della funzione hash.
- Impossibile: 1/(1 - alfa) tende all'infinito per alfa tendente a 1!
- Quello è il numero di confronti nel caso peggiore.
- Quello è il numero medio di confronti per una ricerca con successo.
La visita di un albero per livelli
- è impossibile per ragioni di adiacenza
- fornisce l'ordinamento dei nodi
- fornisce un algoritmo di visita sistematica
- è un'efficiente tecnica di ricerca
Un albero binario di ricerca con n nodi
- ha altezza lg n
- è un albero binario in cui ogni nodo è maggiore del figlio sinistro e minore del destro
- può avere altezza n – 1
- può avere altezza n lg n
- ha altezza lg n
L’altezza media di un albero binario di ricerca con n nodi, costruito in modo casuale, è dell’ordine di
- log n
- n
- n log n
- una costante
Nel caso peggiore, la ricerca su un albero binario di ricerca con n nodi può richiedere un numero di confronti dell’ordine di
- log n
- n
- n log n
- una costante
Le tecniche di bilanciamento degli alberi di ricerca hanno come scopo di
- ottenere un tempo di ricerca costante
- ottenere un tempo di ricerca al più logaritmico
- ottenere un tempo di ricerca lineare
- avere esattamente lo stesso numero di nodi a destra e a sinistra della radice
L'altezza di un RB-albero con n nodi interni
- è lg n.
- è al più 2 lg n.
- è pari alla b-altezza.
- è al più n/2.
Dopo l'inserimento di un nodo in un RB-albero
- possono essere necessarie fino a 2 rotazioni.
- possono essere necessarie anche più di 2 rotazioni.
- basta al più una rotazione.
- se lo zio è nero, basta ricolorare.
Le tecniche di programmazione dinamica
- sono molto faticose per il programmatore.
- sono più efficienti delle tecniche greedy.
- consentono, in generale, di risolvere problemi di ottimizzazione.
- richiedono tempo Omega(n^3).
Le tecniche greedy
- consentono sempre di trovare una soluzione ottima.
- trovano sempre una soluzione, che però può non essere affatto ottima.
- servono a risolvere problemi ricorsivi.
- come dice il nome, richiedono troppe risorse, in generale più della programmazione dinamica.
Perché far studiare i matroidi agli informatici?
- Non l'ho mai capito.
- Perché sono strutture matematiche eleganti e ricche.
- Perché un problema di ottimizzazione che si possa descrivere mediante un matroide pesato ammette una soluzione greedy.
- Perché nei problemi di ottimizzazione che si possono descrivere mediante un matroide pesato le tecniche greedy falliscono.
Il metodo degli accantonamenti per l'analisi ammortizzata
- usa spesso il trucco di attribuire costo ammortizzato nullo alle operazioni il cui costo effettivo è di difficile determinazione.
- determina il costo di n operazioni e poi divide per n.
- prevede l'uso di un contatore binario.
- accantona un potenziale per il costo effettivo.
I B-alberi
- servono a gestire gli alberi in cui il numero dei figli non è determinato.
- consentono di minimizzare il numero degli accessi.
- hanno nodi in cui il numero minimo e massimo dei figli è rigorosamente fissato.
- sono gli alberi di ricerca binaria.
L'altezza di un B-albero contenente n chiavi
- non supera 2 lg n.
- non supera il logaritmo in base t di n.
- è almeno pari al logaritmo in base t di (n+1)/2.
- non supera 3, perché il libro fa vedere che con altezza 2 già ci sono un miliardo di chiavi.
Come conseguenza di una applicazione dell'euristica della compressione dei cammini, per gestire insiemi disgiunti,
- tutto l'albero considerato viene ridotto ad altezza 1.
- il cammino d'accesso viene compresso e quindi occorre determinare la nuova altezza dell'albero.
- l'altezza può ridursi, ma il rango non viene modificato: ecco perché il rango può non coincidere con l'altezza, ma essere più grande.
- gli insiemi disgiunti vengono uniti per rango.
m operazioni su foreste di insiemi disgiunti con le euristiche di unione per rango e compressione dei cammini
- richiedono tempo O(log m)
- richiedono tempo lineare in m
- richiedono tempo O(m α(m, n)), dove α(m, n) è una funzione che cresce molto lentamente con m
- richiedono tempo quadratico in m
* La visita in ampiezza di un grafo qualsiasi, a partire da un nodo s,
- genera un albero di visita, ma, se il grafo non è connesso, non tutti i nodi del grafo saranno nell'albero.
- genera sempre un albero di visita ricoprente il grafo, senza escluderne alcun vertice.
- cerca di allontanarsi prima possibile dal nodo s.
- determina l'ordinamento topologico del grafo.
Le chiamate ricorsive di procedure
- non possono essere eliminate
- possono essere eliminate soltanto usando go to
- in generale possono essere eliminate usando uno stack
- vanno evitate a ogni costo
* Quale delle seguenti affermazioni è vera?
- non è mai possibile accedere ai bit di un byte
- i bit sono unità puramente concettuali
- con il linguaggio C è facile accedere a singoli bit
- per modificare un bit occorre usare l'Assembler