S_02_haar

Wavelet e trasformata di Haar
Una base ortonormale
Multirisoluzione
Image compression e Image denoising
Integral image

Wavelet e trasformata di Haar

Dato un segnale lo "scopo del gioco" è scomporlo come somma di
componenti localizzate in tempo e in frequenza, in particolare la
scomposizione deve essere efficientemente calcolabile. La wavelet più
semplice da calcolare e utilizzare è senza dubbio la wavelet di Haar, la
cui madre è la funzione seguente:

\Psi(t) = \left\{ \begin{matrix} +1 \hfill\quad\textbb{0\leq t<0.5} \\ -1 \hfill\quad\textbb{0.5\leq t<1} \\ 0 \hfill\quad\textbb{altrimenti} \end{matrix} \right.

PS: usare http://www.codecogs.com/latex/eqneditor.php per vedere le eq.

% Haar functions:
Psi = @(t)(double((t>=0&t<0.5)-(t>=0.5&t<1)));
Phi = @(t)(double(t>=0&t<1));

% La wavelet di Haar:
X = -1:0.01:2;
figure; plot(X,Psi(X)); axis equal;
title('Wavelet di Haar');

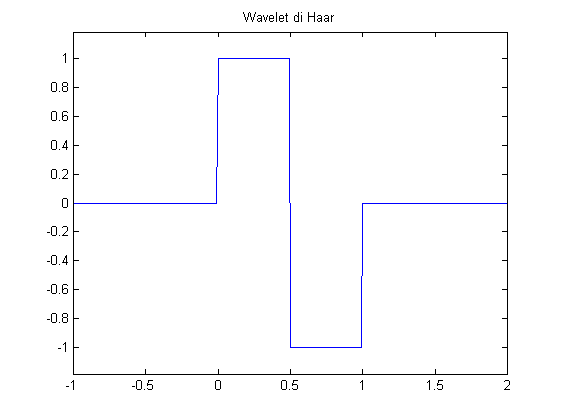
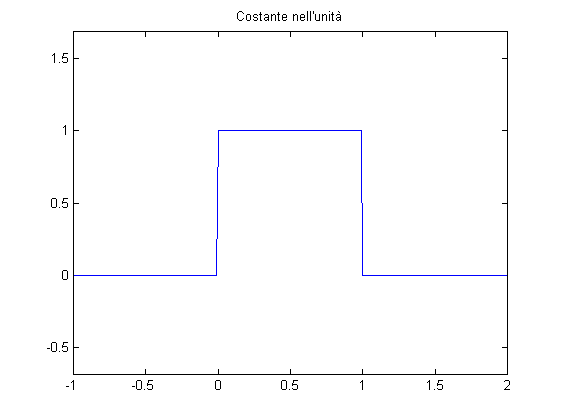
Si tratta di un filtro derivativo (integra a 0), per poter ottenere una
base completa va aggiunta al banco di filtri anche la seguente:

% Costante nell'unità:
figure; plot(X,Phi(X)); axis equal;
title('Costante nell''unità');

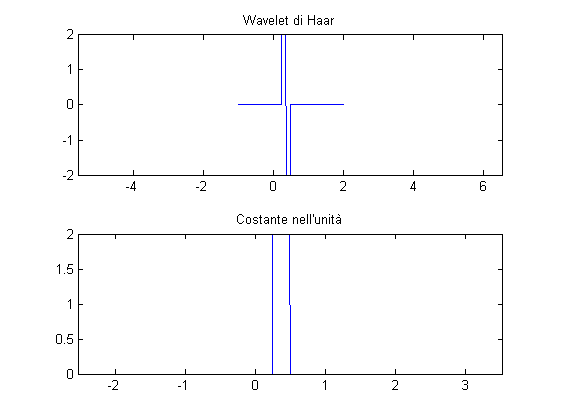
Le traslazioni e scalature per potenze di 2 possono facilmente essere ottenute:

\Psi_{i,j}(t) = \sqrt{2^j}\Psi(2^j t - i)

% Funzioni traslate e scalate:
Psi_ij = @(i,j,t)(sqrt(2.^j).*Psi(2.^j.*t-i));
Phi_ij = @(i,j,t)(sqrt(2.^j).*Phi(2.^j.*t-i));

% Vediamole:
figure;
subplot(211); plot(X,Psi_ij(1,2,X)); axis equal; title('Wavelet di Haar');
subplot(212); plot(X,Phi_ij(1,2,X)); axis equal; title('Costante nell''unità');

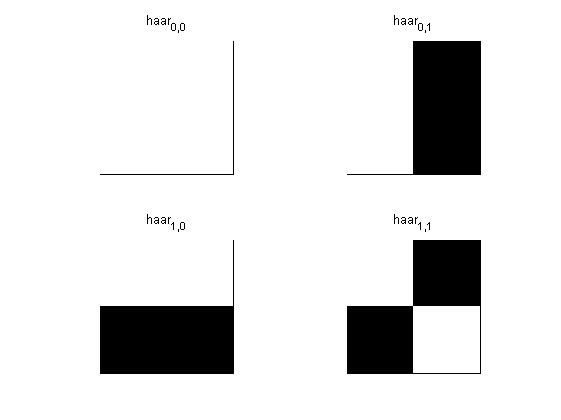
Una base ortonormale

Creiamo una base in \Re^2 con le wavelet di Haar, in particolare ci è
sufficiente combinare Psi e Phi sfruttando la separabilità:

% Genero le basi:
X = 0:0.01:1;
haar00 = Phi(X)'*Phi(X);
haar01 = Phi(X)'*Psi(X);
haar10 = Psi(X)'*Phi(X);
haar11 = Psi(X)'*Psi(X);

% Vediamole:
figure;
subplot(221); imshow(haar00); title('haar_{0,0}');
subplot(222); imshow(haar01); title('haar_{0,1}');
subplot(223); imshow(haar10); title('haar_{1,0}');
subplot(224); imshow(haar11); title('haar_{1,1}');

Verifichiamone l'ortonormalità:

% Tutti i possibili prodotti interni:
haarAll = {haar00,haar01,haar10,haar11};
intProd = zeros(4);
for i=1:4
    for j=1:4
        intProd(i,j) = dot(haarAll{i}(:),haarAll{j}(:));
    end
end

% Vediamole:
fprintf('Prodotti interni:\n');
disp(intProd);

Prodotti interni:
       10000           0           0           0
           0       10000           0           0
           0           0       10000           0
           0           0           0       10000

Decomponiamoci una immagine:

% Carico una immagine:
img = double(imread('cameraman.tif'))/255;

% Creo i filtri 2x2:
haarAll = haarBank(1);

% Applico il banco di filtri:
C = bankApply(img,haarAll);

% Mostro le componenti:
figure;
subplot(121); imshow(cell2mat(C)); title('Decomposizione con Haar (livello 1)');

% Ricostruiamo l'immagine:
subplot(122); imshowscale(sum(cat(3,C{:}),3)); title('Ricostruzione');

Multirisoluzione

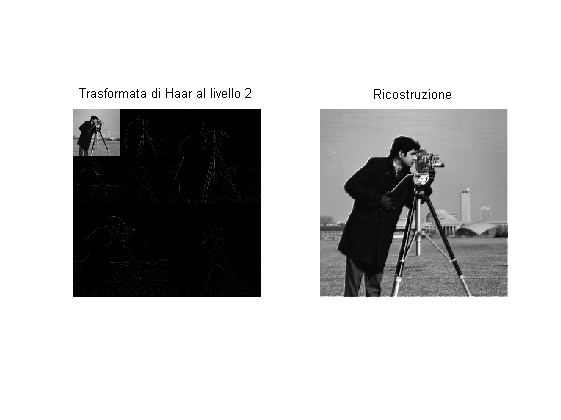
Come visto, una delle 4 componenti ottenute con haar altro non è che la
media viaggiante 2x2, è quindi ammissibile una sua riduzione di scala e
la successiva riapplicazione della stessa decomposizione:

% Riduco di scala:
img2 = C{1}(1:2:end,1:2:end);

% Decompongo nuovamente:
C2 = bankApply(img2,haarAll);

% Provo a ricostruire da zero:
img1 = sum(cat(3,C2{:}),3);
img1 = imresize(img1,2,'bilinear');
C1 = C;
C1{1} = img1;
imgr = sum(cat(3,C1{:}),3);

% Assembo il tutto:
tr2 = cell2mat(C2);
C1{1} = tr2;
tr1 = cell2mat(C1);

% Vediamoli:
figure;
subplot(121); imshow(tr1); title('Trasformata di Haar al livello 2');
subplot(122); imshow(imgr); title('Ricostruzione');

Per sfruttare a pieno la separabilità delle wavelet di Haar, creiamo una
matrice contenente tutte le scale e traslazioni della wavelet 1d, poi
utiliziamo questa matrice sia come banco di filtri orizzontali che
verticali.

Si consideri la matrice definita come segue:

H_i = \left\{\begin{matrix} 1 \hfill\quad\textbb{se\ }i=0 \\ \begin{pmatrix} H_{i-1}\otimes(1,1)\\ 2^{(i-1)/2}I_{2^(i-1)}\otimes(1,-1) \end{pmatrix}\hfill\quad\textbb{altrimenti} \end{matrix}\right.

dove il prodotto di Kronecker A \otimes B è definito a blocchi come:

A \otimes B = \begin{pmatrix} A_{1,1}B & A_{1,2}B \cdots \\ \cdots \\ A_{n,1}B & A_{n,2}B \end{pmatrix}

% La matrice per la nostra immagine:
H = haar(8);

% Vediamola, contiene tutte le wavelet 1d di Haar per scale a potenze di 2:
figure; imshowscale(H);

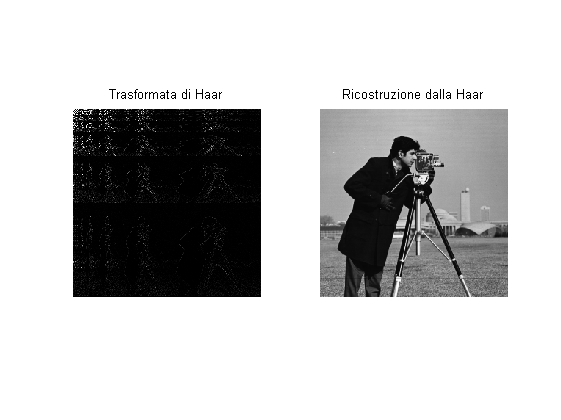
La trasformata di Haar data la matrice H e l'immagine F è definita come:

S = \frac{1}{N} H F H^T

con N lato dell'immagine F; la sua inversa è:

F = \frac{1}{N} H^T S H

Si osservi nella trasformata che l'energia è concentrata in pochi
coefficienti a valori assoluti elevati.

% Init:
N = size(H,1);

% Trasformo:
S = H*img*H'/N;

% Antitrasformo:
F = H'*S*H/N;

% Vediamo:
figure;
subplot(121); imshow(S); title('Trasformata di Haar');
subplot(122); imshow(F); title('Ricostruzione dalla Haar');

Osserviamo meglio cosa è successo identificando i coefficienti a valori
superiori a una certa percentuale rispetto al massimo:

% Li identifico:
perc = 0.0005;
mask = S > max(abs(S(:)))*perc;

% Vediamo:
figure; imshow(mask); title('Coefficienti sopra lo 0.05% del massimo');

Image compression e Image denoising

Le wavelet trovano applicazione, oltre che nella caratterizzazione di
punti nelle immagini (a scopo di classificazione/clustering) nella
compressione e riduzione di rumore nelle immagini, facciamo un esempio
usando le wavelet di Haar: il seguente filmato mostra l'approssimazione
ottenuta codificando un'immagine tramite trasformata di Haar eliminando
una percentuale (decrescente) di coefficienti a valore basso.

img = double(imread('cameraman.tif'))/255;
S = haarTransf(img);
figure;
for perc=2.^(0.1:-0.5:-10)
    mask = abs(S)<=perc*max(abs(S(:)));
    S2 = S; S2(mask) = 0;
    F2 = haarInv(S2);
    clf; imshow(F2); drawnow; pause(0.1);
end

Integral image

Le wavelet di Haar applicate a una immagine per una determinata
posizione e scala producono come risposta la somma dei valori dei pixel
contenuti in aree rettangolari, per poter calcolare rapidamente la
risposta di una immagine ad una determinata wavelet di haar è
indispensabile fornire un algoritmo che calcoli questa somma in maniera
efficiente, in particolare è indispensabile produrre un algoritmo che
permetta di spostare la complessità computazionale dal calcolo di una
singola risposta ad una operazione di preprocessing. L'integral image è
uno immagine calcolabile in tempo lineare nel numero di pixel, tramite
essa è possibile calcolare la somma di valori di pixel contenuti in
rettangoli arbitrari in tempo costante (3 operazioni di somma/sottrazione
in tutto). L'integral image di una immagine I è definita come segue:

II(x_0,y_0) = \sum_{x=0}^{x_0} \sum_{y=0}^{y_0} I(x,y)

In una dimensione tali somme cumulate sono calcolabili iterativamente
seguendo la regola di ricorsione:

II(t) = \left\{ \begin{matrix} I(0) \hfill\quad\textbb{per\ } t=0 \\ I(t-1)+I(t) \hfill\quad\textbb{altrimenti} \end{matrix} \right.

In Matlab la funzione cumsum svolge questo compito. Per ottenere il
risultato desiderato su una immagine cumsum deve essere applicata a tutte
le righe e poi a tutte le colonne.

% Somma cumulata per righe e poi per colonne:
iimg = cumsum(img,2);
iimg = cumsum(iimg,1);

% Vediamola:
figure; imshowscale(iimg);

Per quanto non visibile a occhio, questa immagine integrale contiene le
informazioni che permettono di calcolare in maniera rapida la somma in un
rettangolo di dimensione arbitraria:

% Funzione di somma in un rettangolo:
sumRect = @(iimg,p1,p2)(iimg(p2(2),p2(1))-iimg(p1(2)-1,p2(1))-iimg(p2(2),p1(1)-1)+iimg(p1(2)-1,p1(1)-1));

% Un rettangolo di esempio:
rect = [10,30,100,100];

% Somme in quel rettangolo:
sum1 = sumRect(iimg,rect(1:2),rect(1:2)+rect(3:4));
sum2 = sum(sum(imcrop(img,rect)));

% Verifichiamo:
fprintf('Differenza: %d\n', abs(sum1-sum2));

Differenza: 1.818989e-012

Questa tecnica permette di calcolare efficientemente qualunque
espressione del tipo \sum_{R} f(x,y) dove R è un rettangolo, ottenendo ad
esempio le funzioni di dsitools fastcorr2Plane, fastsad2Plane e
fastssd2Plane. Come building-block si veda imintegrate.

% Vediamolo:
figure;
subplot(121); imshow(img);
subplot(122); imshow(imintegrate(img,50));

Contents

Wavelet e trasformata di Haar

Una base ortonormale

Multirisoluzione

Image compression e Image denoising

Integral image