Wavelets

Ttrasformata di Fourier e trasformata coseno hanno dimostrato efficacia
per l'analisi in frequenza dei segnali, sfortunatamente però osservando
il segnale nel dominio spaziale non si hanno informazioni relative alla
frequenza, mentre nel dominio della frequenza non si hanno informazioni
spaziali, per mantenere entrambe le informazioni dobbiamo tassellare il
piano della spazio-frequenza, le Wavelet rappresentano proprio
tassellazioni ammissibili del piano di spazio-frequenza che permettano la
ricostruzione esatta del segnale di partenza.

PS: usare http://www.codecogs.com/latex/eqneditor.php per vedere le eq.

Contents

Primi esempi intuitivi

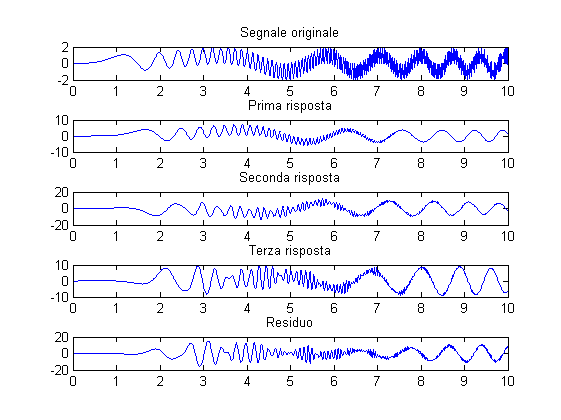
Intuitivamente, un filtro passa-basso applicato a un segnale genera un
segnale contenente le sole basse frequenze spazialmente localizzate, il
residuo contiene le altre frequenze... che a loro volta possono essere
separate nello stesso modo:

% Genero un segnale:
X = 0:0.01:10;
sig = sin(((X/5).^2).*X) + sin((X.^2).*X);

% Preparo un filtro passa-basso:
H1 = gauss(-5:0.1:5,0.15,0,false);

% Separo le basse frequenze da quelle più alte:
ans1 = filter(H1,1,sig);
sig1 = sig - ans1;

% Separo Ancora:
H2 = H1(1:2:end);
ans2 = filter(H2,1,sig1);
sig2 = sig1 - ans2;

% Separo Ancora:
H3 = H2(1:2:end);
ans3 = filter(H3,1,sig2);
sig3 = sig2 - ans3;

figure;
subplot(511); plot(X,sig); title('Segnale originale');
subplot(512); plot(X,ans1); title('Prima risposta');
subplot(513); plot(X,ans2); title('Seconda risposta');
subplot(514); plot(X,ans3); title('Terza risposta');
subplot(515); plot(X,sig3); title('Residuo');

Sempre intuitivamente, per ottenere un filtro con risposta localizzata
sia spazialmente che nel dominio della frequenza è necessario
identificare una trasformata che si avvalga di atomi (componenti) a loro
volta localizzate sia spazialmente che nelle frequenze. La trasformata di
Fourier utilizza come atomi le armoniche e^{iwt} di pulsazione w,
infinitamente localizzate nella frequenza ma non localizzate nel tempo.

Sempre intuitivamente, la localizzazione nel tempo la si può ottenere
"pesando localmente" il segnale:

 f_u(t) = \int_{-\infty}^{+\infty} \hat{f}(w)g(t-u)e^{iwt}dw

In generale, si consideri una trasformata come la proiezione di una
funzione f(t) su una base dello spazio di Hilbert in cui la funzione
stessa vive (vedremo quale di preciso, in particolare le funzioni
appartenenti allo spazio considerato sono continue e derivabili a
tratti), ovvero:

f(t) = \int_{-\infty}^{+\infty} \left< f,\Psi_w \right> \Psi_w dw

dove la singola componente \Psi(w) è "pesata" dal prodotto interno:

\left< f,\Psi_w \right> = \int_{-\infty}^{+\infty} f(t)\overline{\Psi_w(t)} dt

Se quindi si intendono evidenziare caratteristiche localizzate
simultaneamente nel tempo e nella frequenza bisognerà scegliere \Psi
opportunamente.

Nota: una gaussiana è localizzata sia nel dominio del tempo che della
frequenza (la trasformata di una gaussiana è una gaussiana). Un approccio
consiste nel traslare una gaussiana (o alra funzione) sia nel dominio del
tempo che della frequenza, considerato che una traslazione di \xi in
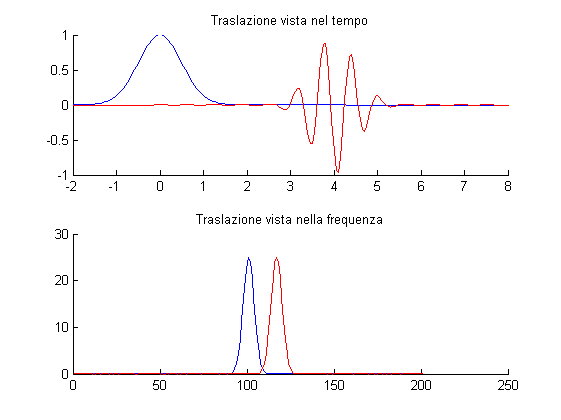
frequenza si ottiene moltiplicando per e^{i\xi t}, otteniamo:

\Psi_{u,\xi} = g(t-u)e^{i\xi t}

con g() gaussiana non normalizzata.

% Creo una gaussiana:
sigma = 0.5;
g = @(t)(gauss(t,sigma,0,false));

% La traslo in spazio e frequenza:
u = 4; xi = 10;
g2 = @(t)(g(t-u).*exp(1i.*xi.*t));

% Vediamo cosa salta fuori:
X = -2:0.05:8;
figure;
subplot(211); hold on; title('Traslazione vista nel tempo');
plot(X,g(X),'b',X,real(g2(X)),'r');
subplot(212); hold on; title('Traslazione vista nella frequenza');
plot(abs(fftshift(fft(g(X)))),'b');
plot(abs(fftshift(fft(g2(X)))),'r');

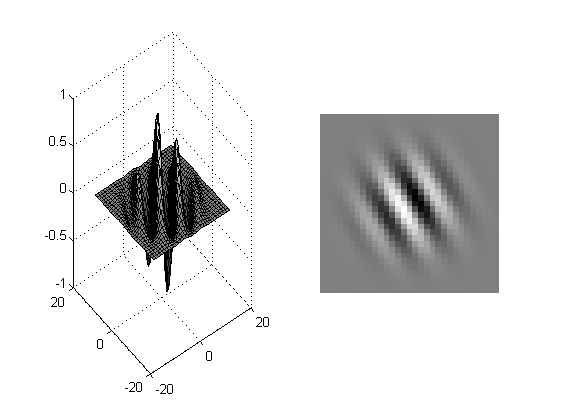
Gli atomi ottenuti prendono il nome di filtri di Gabor, in 2 dimensioni
i filtri di Gabor hanno più gradi di libertà, in particolare 2DoF per la
traslazione in spazio, 2DoF per la traslazione in frequenza, 1DoF per la
rotazione e 1DoF per la fase (presente anche in 1d). Date (x,y), le
coordinate di un punto del piano, per la rotazione si ha:

(x',y') = \left(x cos(\theta) + y sin(\theta), y cos(\theta) - x sin(\theta) \right)

da cui il filtro di Gabor 2d con orientazione theta:

\Psi_{\theta,\vec{u},\xi}(x,y) = g(\|(x',y')-\vec{u}\|) e^{i\xi x'}

% Init:
sigma = 5;
xi = 1;
theta = -30*pi/180;
[X,Y] = meshgrid(-3*sigma:3*sigma);

% Ruotiamo il sistema di riferimento:
xp = X.*cos(theta) + Y.*sin(theta);
yp = Y.*cos(theta) - X.*sin(theta);

% Calcoliamo separatamente gaussiana e traslazione in frequenza:
G = gauss(sqrt(xp.^2 + yp.^2), sigma, 0, false);
Gw = exp(1i*(xi*xp + pi/2)); % Notare la fase pi/2 per ottenere un filtro derivativo

% Il filtro di Gabor:
Psi = Gw.*G;

% Vediamolo:
figure;
subplot(121); title('Filtro di Gabor 2d'); surf(X,Y,real(Psi));
subplot(122); title('Filtro di Gabor 2d'); imshowscale(real(Psi));

Trasformata di Fourier "a finestra"

Unendo i concetti precedenti è possibile ottenere una trasformata di
Fourier localizzata in spazio e frequenza come proiezione di una funzione
su un atomo:

Sf(u,\xi) = \left< f, \Psi_{u,\xi} \right> = \int_{-\infty}^{+\infty} f(t)g(t-u)e^{-i\xi t} dt

Grazie a questa trasformata è possibile osservare la variazione delle
componenti in frequenza al variare dell'istante di osservazione.

% Init:
X = 1:1000;
sigma = 3;

% Una funzione:
f_t = sin(X.*((1+50*X/numel(X)).^2*2*pi/20000));

% Per ogni u:
Sf = zeros(numel(X));
for u=1:numel(X)
    % La peso con una gaussiana:
    f_t_g = f_t.*gauss(X,sigma,u,false);

    % Trasformata di fourier:
    Sf(:,u) = fftshift(fft(f_t_g));
end

% Vediamola:
figure; imshowscale(abs(Sf));

Heisenberg boxes

Si osservi che ogni filtro locale in tempo e frequenza occupa un
rettangolo nel piano tempo-frequenza che viene così tassellato, si può
dimostrare che ogni rettangollo non può avere area minore di 1/2, ovvero
non esistono atomi il cui supporto in tempo-frequenza ha area minore di
questo valore. Da ciò se ne deduce che l'aumento in risoluzione in un
dominio (ad esempio nel tempo) ne riduca la risoluzione nell'altro (ad
esempio in frequenza).

% Un banco completo di filtri di Gabor:
bank = gaborBank((0:360/8:359)*pi/180,2.^(-5:-1),true);
contr = zeros(size(bank{1}));
for i=1:numel(bank)
    contr = contr + fftshift(fft2(bank{i}));
end
figure; imshowscale(abs(contr));
% for i=1:numel(bank); figure; imshowscale(bank{i}); end

Dai filtri a finestra alle wavelet

La tassellazione del piano tempo-frequenza della trasformata di Fourier
a finestra è uniforme, per poter operare in modalità multiscala è invece
utile tassellare tale piano in maniera non uniforme, ovvero aumentando la
risoluzione spaziale per le frequenze più alte, questo risultato può
essere ottenuto mantenendo fissa una wavlet detta "madre" e scalandola
nel dominio del tempo:

Wf(u,s) = \left< f, \Psi_{u,s} \right> = \int_{-\infty}^{+\infty} f(t)\frac{1}{\sqrt{s}}\overline{\Psi\left(\frac{u-t}{s}\right)} dt

% Un banco completo di wavelet di Gabor:
bank = gaborBank((0:360/8:359)*pi/180,2.^(-5:-1));
contr = zeros(size(bank{1}));
for i=1:numel(bank)
    contr = contr + fftshift(fft2(bank{i}));
end
figure; imshowscale(abs(contr));
% for i=1:numel(bank); figure; imshowscale(bank{i}); end

Applicazione di esempio

In questo esempio proviamo ad utilizzare i pochi strumenti a
disposizione per affrontare un problema reale (ottenendo un risultato non
eccezionale e sicuramente migliorabile con un po' di strumenti in più).

Scopo del gioco è ritrovare un punto di interesse segnato su una
immagine, allinterno di una seconda immagine differente dalla prima, in
particolare un punto dell'occhio dove sia presente una struttura di bordi
identificabile tramite filtri orientabili come quelli di Gabor.

% % Caricamento delle immagini:
% img = imread('http://farm4.static.flickr.com/3024/3070506253_842da24afe.jpg');
% img2 = imread('http://media-2.web.britannica.com/eb-media/21/79821-004-507765DA.jpg');
% img = imtype(img,'gF');
% img2 = imtype(img2,'gF');
%
% % Selezione del punto di interesse:
% figure; imshow(img);
% p = getpoints(1);

% Carico localmente i dati:
img = imtype(imread('training.jpg'),'gF');
img2 = imtype(imread('testing.jpg'),'gF');
p = [120;284];

% Preparazione dei filtri:
bank = gaborBank;
bank = bank(1:end-1);

% Caratterizzazione del punto di interesse:
v = real(bankApply(img,bank,p));
v = reshape(v,[1,1,numel(bank)]);

% Applicazione dei filtri all'intera immagine:
C = bankApply(img2,bank);
V1 = real(cat(3,C{:}));

% % Calcolo della distanza coseno:
% v = v/norm(v(:));
% normV1 = sqrt(sum(V1.^2,3));
% V1normalized = V1 ./ repmat(normV1,[1,1,numel(bank)]);
% cos_theta = sum(V1normalized.*repmat(v,[size(V1,1),size(V1,2)]),3);
% dist = (1-cos_theta)/2;

% Distanza euclideea tra features:
dist = sqrt(sum((repmat(v,[size(V1,1),size(V1,2)])-V1).^2,3));

% Ottenimento dei punti con minore distanza coseno:
% [val,pos] = min(dist_cos(:));
[val,pos] = sort(dist(:));
[y,x] = ind2sub(size(dist),pos);

% Vediamo il risultato:
figure;
subplot(121); imshow(img); hold on; plotpoints(p,'ro');
subplot(122); imshow(img2); hold on; plotpointsLabels([x(1:10),y(1:10)]','ro');

Published with MATLAB® 7.13