Active Shape Models
L'analysis di Procruste offre strumenti che permettono di misurare distanze e trasformare le forme in maniera tale da allinearle su uno stesso spazio, su un manifold in cui si abbia invarianza per similarità. Una volta che le forme a N punti (dN gradi di libertà) sono state proiettate su questo manifold a dimensionalità più bassa, possono essere utilizzate come esempi per la stima di statistiche sulla popolazione, ad esempio per ottenere delle statistiche sulla forma della bocca umana a partire da un certo numero di campioni (quanti campioni siano necessari dipende sia dalla variabilità della forma che dal task prefisso).
In particolare, una forma definita da N punti in uno spazio a d dimensioni ha dN gradi di libertà di cui d sono relativi alla posizione, uno alla scala e d(d-1)/2 alla rotazione, si hanno quindi:
d N - d - 1 - \frac{d(d-1)}{2}gradi di libertà associati alla forma vera e propria (ovvero dopo aver eliminato posizione scala e rotazione).
Uno degli strumenti più utilizzati nel machine-learning è la Principal Component Analysis, ovvero la scomposizione dei dati in media e direzioni di massima varianza. Questo strumento, applicato alle forme, permette di deformare un modello di forma per poterlo adattare a un'immagine, quindi si offre come valido strumento di segmentazione. Uno strumento simile sono gli snakes, ovvero spezzate deformabili in cui i vincoli utilizzati per guidare la convergenza verso un edge di interesse sono di livello più "basso", ovvero riguardano solamente la distanza tra punti e la curvatura, per questo motivo gli ASM vengono anche chiamati snake a semantica di forma.
Contents
PCA
Per poter costruire uno strumento basato sugli active shape models è indispensabile comprendere a fondo come funzioni lo strumento PCA, in particolare si ipotizzi di avere un dataset X (punti per colonna):
% Generazione di punti nel piano: N = 1000; theta = pi/6; R = [cos(theta),sin(theta);-sin(theta),cos(theta)]; X = R*diag([1,4])*randn(2,N) + repmat([10;20],[1,N]); % Vediamoli: figure; plotpoints(X,'r.'); axis equal;
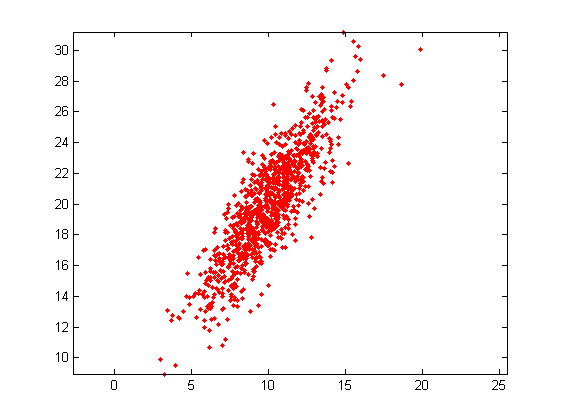
Per prima cosa separiamo la media ottenendo dati centrati nell'origine:
% La media: mu = mean(X,2); % Sotrtaiamola dai dati: Xc = X - repmat(mu,[1,size(X,2)]);
Il dataset ottenuto è distribuito come una normale multivariata a media nulla, purtroppo però le direzioni di massima varianza non sono allineate agli assi, per ottenere questo risultato è necessaria una rotazione. La matrice di rotazione di interesse può essere ottenuta costruendo un sistema di riferimento sui dati che ricerchi le direzioni di massima varianza e le sottragga una per una.
Una possibilità per la scomposizione della matrice X_c dei dati centrati è considerarla come un insieme di esempi estratti da una normale multivariata isotropa e successivamente trasformati con una matrice di scalatura e rotazione, ovvero:
X_c = R S X_{gi}con X_{gi} matrice degli esempi estratti dalla normale isotropa. Si consideri ora la matrice di covarianza di X_c (scalata):
(N-1)\Sigma = \sum_{i=1}^N (x_i-\mu)(x_i-\mu)^T = X_c X_c^Tda cui:
(N-1)\Sigma = (X_{gi}^T S R^T R S X_{gi})^T = X_{gi}^T S^2 X_{gi}per la simmetria di S e \Sigma e per l'ortonormalità di R.
Si osservi che il problema precedente può essere interpretato come un
problema di identificazione degli autovalori (in S^2) e degli autovettori
(in X_{gi}), risolvibile quindi con una eigenvalue decomposition. Si
osservi che è possibile ottenere una implementazione più efficiente
utilizzando la Singular Value Decomposition anziché la
Eigen Decomposition.% Stimiamo la matrice di covarianza: Sigma = Xc*Xc'; % Risolviamo il problema degli autovalori/autovettori: [V,D] = eig(Sigma); % Proiettiamo i punti su di essi: Xp = V'*Xc; % Vediamone il risultato: figure; plotpoints(Xp,'r.'); axis equal;
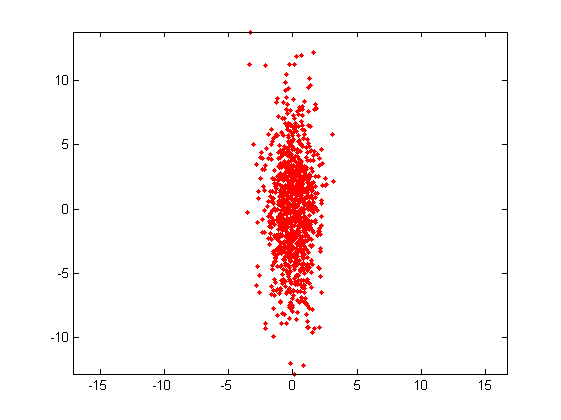
Chiaramente può essere di interesse passare da una rappresentazione all'altra, facciamolo in particolare per gli assi cartesiani:
% Gli assi: Assi = [eye(2),-eye(2)]*3/sqrt(D(1)); % Stimiamo la trasformazione come radice \sqrt{V D V'} = V D^{1/2}: T = V*D^(1/2); % La trasformazione e la traslazione: Assit = T*Assi + repmat(mu,[1,size(Assi,2)]); % Mostriamo il risultato: figure; hold on; plotpoints(X,'b.'); plotpoints(Assit(:,[1,3]),'r-o'); plotpoints(Assit(:,[2,4]),'r-o'); axis equal;
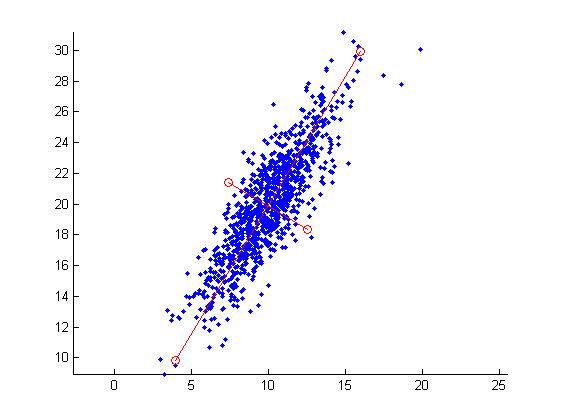
ASM
Un modello per gli ASM si ottiene allineando le forme alla forma media, generando vettori in 2N dimensioni semplicemente "srotolando" le coordinate dei punti di ogni forma allineata, e alla fine calcolando la PCA di questi vettori. Il modello ottenuto consiste di media, covarianza e componenti principali su cui muoversi (ordinate dalla varianza massima alla varianza mimnima).
% Caricamento dei dati allineati con la Procrustes analysis: load bocche; N = size(W,1); % PCA delle bocche: W = [real(W);imag(W)]; mu = mean(W,2); Wc = W - repmat(mu,[1,size(W,2)]); [V,D] = eig(Wc*Wc'); % Una bocca sintetica: C = sqrt(diag(D))/6; bocca = V*D^(1/2)*C + mu; bocca = [bocca(1:N),bocca(N+1:end)]'; % Vediamola: alpha = -2.7261; R = [cos(alpha),sin(alpha);-sin(alpha),cos(alpha)]; figure; plotshape(R*bocca,'r-'); axis equal ij;
Warning: Imaginary parts of complex X and/or Y arguments ignored
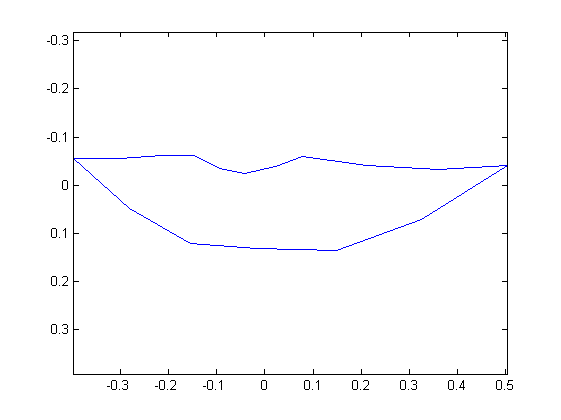
Allineamento automatico
L'allineamento automatico (previo inizializzazione della posa, eseguita manualmente in questo esempio) avviene iterativamente. Lo scopo del gioco è allineare la forma all'immagine facendo avvicinare i landmark a zone di interesse (ad esempio in cui sono presenti dei bordi), mantenendo comunque la forma sul sottospazio identificato per essa (es.: sottospazio delle bocche). Il processo iterativo consiste nella minimizzazione di una funzione energia che dipende ad un immagine di valori di energia associati ai singoli pixel, nel nostro caso i bordi della mouthmap rappresentano le zone a bassa energia (alti valori nella nostra immagine), mentre l'ASM verrà utilizzato per proiettare la forma ottenuta spostando separatamente i punti sul sottospazio delle forme di interesse.
% Inizializzazione: load bocche; global img i; img = imtype(imread('boccaEsempio.jpg'),'cF'); % Posa inizializzata manualmente: % f=figure; imshow(img); pts=getpoints(2); close(f); pts = [40,265;88,94]; % Buona. % pts = [30,258;74,124]; % Sufficiente. % pts = [27,247;62,145]; % Insufficiente. mu = ASM.getMean(); alpha = atan2(pts(2,2)-pts(2,1),pts(1,2)-pts(1,1)) - atan2(mu(2,11)-mu(2,1),mu(1,11)-mu(1,1)); scale = norm(pts(:,1)-pts(:,2))/norm(mu(:,1)-mu(:,11)); trasl = mean(pts,2); T = mksimilarity(scale,alpha,trasl); % Trasformo: mu = points2dnormalize(T*points2domogenize(mu)); mu2 = mu; % Frame di partenza: figure; imshow(img); hold on; plotshape(mu); axis equal ij; % Immagine dei bordi: edges = gaussianDerivative(mouthmap(img)); % Costruisco uno snake: sn = snake_belief(mu,'closed',true,'rad',10,'frel',[]); % Controllo la varianza ritenuta nel modello di forma: ASM.setVar(0.8); % Iterazioni di convergenza della forma: for i=1:20 % Disegno il frame precedente: drawnow; pause(0.1); % Evoluzione dello snake: sn.evolve(edges); % Forzatura della forma: mu = ASM.projectShape(sn.getPoints()); % Questo frame: clf; imshow(img); hold on; sn.plot(true); plotshape(mu,true,'r-.'); % Ripristino dello snake: sn.setPoints(mu); end plotshape(mu2,true,'c-'); % Tengo i punti allineati per dopo: sn.evolve(edges); ptsAllineati = sn.getPoints();
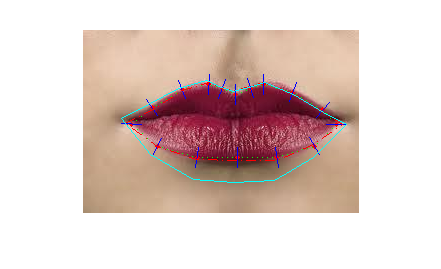
Generiamo nuove bocche
La generazione di nuove immagini per un soggetto, oltre all'ovvio scopo ludico, permette di deformare un modello comprensivo di aspetto e di confrontarlo con una nuova immagine allo scopo di fittarne non solo i parametri di forma ma anche quelli di aspetto. Questo strumento è quindi la base della tecnica nota come Active Appearance Model (AAM), in essa infatti a tempo di addestramento si deformano le immagini del soggetto affinché fittino il modello medio, successivamente viene applicata alle immagini sintetizzate la PCA come visto in precedenza per la forma, ottenendo quindi un modello di aspetto "deformabile" quanto quello di forma. Al termine dell'addestramento il modello di forma e quello di aspetto possono essere utilizzati assieme per produrre nuove immagini del soggetto.
Vediamo come generare efficientemente una nuova immagine di un soggetto deformandone il contenuto come descritto dal modello di forma:
% Params: scale = 300; load bocche; % Una forma di bocca ottenuta dal modello scegliendo i primi parametri: ASM.setAlpha(-2.7261); alpha = ASM.getAlpha(); R = [cos(alpha),sin(alpha);-sin(alpha),cos(alpha)]; % - Bocca media: % mu = scale*R*ASM.getMean(); % - Bocca sorridente: model = ASM.getModel(); mu = scale*R*ASM2dMorph(model,[-model.L(1)*10,-model.L(2)*10]); %- mu = ceil(mu - repmat(min(mu,[],2),[1,size(mu,2)]) + 1); % Ottengo la bocca media e la triangolo: tri = delaunay(mu(1,:),mu(2,:)); % Generiamo l'immagine degli indici: sze = ceil(max(mu,[],2)); w = sze(1); h = sze(2); [X1,Y1] = meshgrid(1:w,1:h); Inds = zeros(h,w,'uint8'); for i=1:size(tri,1) % Trovo gli indici dei pixel interessati da questo triangolo: pts = impxgen_triangle(mu(:,tri(i,:))); I = sub2ind(size(Inds),pts(2,:),pts(1,:)); % Scrivo nell'immagine degli indici: Inds(I) = i; end % Vediamoli: figure; subplot(121); hold on; plotpoints(mu,'r.'); triplot(tri,mu(1,:),mu(2,:)); axis equal ij off; subplot(122); imshowscale(Inds); hold on; title('Indici dei triangoli');
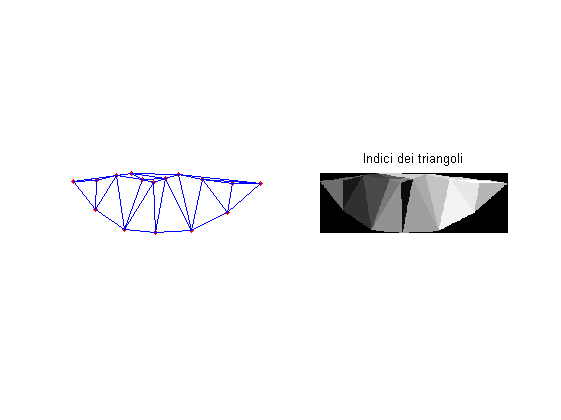
Deformiamo una immagine di esempio tramite una omografia per triangolo, ovvero per ogni punto di destinazione nel modello di bocca deve esserne calcolato il punto di provenienza dall'immagine di interesse, per poi stimrne i valori dei pixel per i canali RGB tramite interpolazione.
% Carico l'immagine: % img = imread('https://encrypted-tbn1.google.com/images?q=tbn:ANd9GcRJWjh_Ya_ZHFPj8zQ4fMGbQ6AZZ97JqsvM-tT7XRnM7wVtoilU'); img = imtype(imread('boccaEsempio.jpg'),'cF'); % Ottengo i punti allineati della bocca: % f = figure; imshow(img); pts = getpoints(16); close(f); load boccaEsempioPoints; % pts = ptsAllineati; % Inizializzo: [X,Y] = meshgrid(1:size(img,2),1:size(img,1)); img2 = zeros([size(Inds),3]); mask = Inds>0; allPts = zeros(2,sum(mask(:))); last = 0; inds = zeros(1,size(pts,2)); % Trasformo i punti: for i=1:size(tri,1) % Ottengo i punti: src = mu(:,tri(i,:)); dest = pts(:,tri(i,:)); % Calcolo l'omografia: H = affineFrom3pts(src,dest); % Ottengo i punti da trasformare: mask1 = Inds==i; p = [X1(mask1),Y1(mask1)]'; % Trasformo e salvo: range = last+1:last+size(p,2); allPts(:,range) = points2dnormalize(H*points2domogenize(p)); inds(range) = p(1,:)*h + p(2,:) + 1; last = last + size(p,2); end % Riordino: [vals,inds] = sort(inds); allPts = allPts(:,inds); % Ne ottengo il colore (interpolando): mode = 'bilinear'; %'nearest'; reds = interp2(X,Y,img(:,:,1),allPts(1,:),allPts(2,:),mode); greens = interp2(X,Y,img(:,:,2),allPts(1,:),allPts(2,:),mode); blues = interp2(X,Y,img(:,:,3),allPts(1,:),allPts(2,:),mode); img2(cat(3,mask,mask,mask)) = cat(3,reds,greens,blues); % Vediamola: figure; subplot(121); imshow(img); title('Immagine di partenza'); subplot(122); imshow(img2); title('Risultato');

Altri modelli di forma
Gli ASM sono modelli statistici di forma, chiaramente è possibile costruire modelli statistici differenti (ad esempio non basati sull'assunzione di gaussianitò dalla PCA). Gli snakes sono un esempio di modello di forma molto semplice e generale, non legato a una singola forma ma solamente alla smoothness della stessa.
Uno snake è una spezzata, formata da un numero arbitrario di punti N>1, che viene inizializzata un una qualche posizione sull'immagine e che si muove su di essa alla ricerca del soggetto di interesse, di solito un bordo. Scopo del gioco: definire e minimizzare una funzione energia dipendente dall'immagine e dal modello di forma stesso. Come in molti modelli avviene la funzione energia ha due termini che definiscono l'attinenza ai dati (energia esterna) e l'attinenza al modello (energia interna, smoothness nel nostro caso). La prima viene calcolata nel vicinato dei punti dello snake, una tecnica comune consta nel misurare l'energia come negativo dell'integrale dell'immagine dei bordi sullo snake (o somma sui soli punti). La seconda invece dipende solamente dalla forma dello snake, e consta di differenti termini: energia di continuità e di curvatura:
E_{tot} = \alpha E_I + \beta E_c + \gamma E_kdove un esempio di implementazione è:
E_I = \sum_{i=1}^N I_{dg}(p_i)
E_c = \sum_{i=1}^{N-1} d(p_i,p_{i+1})^2
E_k = \sum_{i=2}^{N-1} |d(p_i,p_{i+1})-d(p_i,p_{i-1})|^2definendo I l'immagine filtrata con la derivata della gaussiana (orizzontale e verticale sommati in valore assoluto), p_i i punti dello snake, d() la funzione distanza euclidea.
In particolare su ogni punto p_i: E_{I,i} è l'energia dovuta alla
immagine in quel punto, ad esempio il valore del pixel dopo aver
applicato un edge detector; E_{c,i} è l'energia che mantiene uniformità
di spaziatura nello snake, E_{k,i} evita che lo snake si arrotoli su sé
stesso.Esempi su: http://users.ecs.soton.ac.uk/msn/book/new_demo/Snakes/
% Globali solo per la callback: global hP; % Carico una immagine: img = imtype(imread('cameraman.tif'),'gF'); % Alcuni parametri: M=10; closed=false; withFixed=false; % Ottengo i punti: figure; imshow(img); hold on; %oP = getpoints; oP = [35,17,81;133,95,49]; if closed; oP=[oP,oP(:,1)]; end N=size(oP,2); % Genero altri punti: P = []; for i=1:N-1 % Un segmento alla volta: nP = [oP(1,i):(oP(1,i+1)-oP(1,i))/M:oP(1,i+1) oP(2,i):(oP(2,i+1)-oP(2,i))/M:oP(2,i+1)]; P = [P,nP(:,1:end-1)]; end if ~closed; P=[P,oP(:,end)]; end % Se vengono fissati dei punti (noti) lo snake lavora molto meglio: if withFixed if closed; fixed=[repmat([true,false(1,M-1)],[1,N-1])]; else fixed=[repmat([true,false(1,M-1)],[1,N-1]),true]; end else fixed = []; end % Creo lo snake snake: sn = snake_belief(P,'fixed',fixed,'closed',closed,'rad',20,'dt',0.1); % Lavoriamo con la norma del gradiente (bordi): [dx,dy] = gradient(img); ref = sqrt(dx.^2 + dy.^2); % Mostriamo l'evlouzione dello snake: hP = P; cbk = @(sn,ref)(eval(['global img hP i; hP=cat(3,hP,sn.getPoints());', ... 'cla; imshow(img); hold on; ', ... 'for i=1:size(hP,3); plotpoints(hP(:,:,i),''c-''); end; ', ... 'sn.plot(true); drawnow;'])); sn.evolve(ref,50,0.01,cbk);

Un altro modello deformabile di forma si ottiene imponendo dei vincoli geometrici specifici ottenuti da un modello geometrico vincolato (si veda GeoML o KSEG).
In un modello geometrico vincolato esistono dei parametri liberi e delle entità geometriche (o altri parametri) vincolate ad essi, in più entità geometriche possono generare altre entità geometriche vincolate ad esse dando vita al modello.
Per eseguire quanto segue i file jar in questa cartella devono essere nel classpath (si usi "edit classpath.txt" e dopo aver salvato si riavvii Matlab).
% Carico il modello geometrico: [model,free,freeStruct] = GeoMLParseModel('bocca'); % Generiamo i punti per il modello di default: pts1 = GeoMLIterate(model,true,'real');
Scopo di un modello deformabile di forma è deformarlo, i parametri di questo modello sono i seguenti:
H,L: Altezza e larghezza. Asx,Bsx Adx,Bdx: Coefficienti liberi delle cubiche superiori. Xsx,Ysx Xdx,Ydx: Punti liberi dei lati della bocca. Alow: Coefficiente libero della parabola infreriore.
% Modifichiamo il modello: freeStruct.H.setValueUpdate(10); freeStruct.Alow.setValueUpdate(-0.02); pts2 = GeoMLIterate(model,true,'real'); % Vediamoli: figure; hold on; plotpoints(pts1,'b-'); axis equal ij off; plotpoints(pts2,'r-'); axis equal ij off;

Per "giocare" con questo modello (o crearne di vostri, si veda GeoML in dsiJtools), bisogna eseguire i seguenti comandi:
import com.dsi.libs.geoml.terminals.GeoMLModelViewer; GeoMLModelViewer.main('');
si carichi la bocca con X=0, Y=0 e Zoom=5.. poi si faccia pan.
PS.: L'interfaccia "spartana" non permette editing visuale, GeoML è nata per essere usata automaticamente da codice Matlab o Java, non per essere un tool interattivo (ma prima o poi lo diventerà).
NOTA: Il processo di acquisizione dati per il training è molto più complesso, una volta accumulati questi è comunque possibile usare tecniche statistiche come la (PCA o altro) per manipolare "intelligentemente" i parametri, in alcune applicazioni questo tipo di strumento è più efficace, spesso un ASM però offre più flessibilità e semplicità di utilizzo.