Analisi di forma

Utilizzando tecniche spesso scelte e adattate ai singoli casi, è
possibile estrarre punti di interesse da immagini di soggetti noti
(occhi, facce, bocche, ...). Una volta identificati i punti di interesse
è possibile operare tramite algoritmi basati sulla geometria e sulla
statistica.

I punti di interesse vengono chiamati landmark, nei nostri esempi i
landmark sono stati selezionati a mano, cosa che accade spesso in
applicazioni di tipo medicale, la localizzazione automatica dei landmark
è un problema che non affronteremo in questo "capitolo", rimandando a
strumenti di caratterizzazione e classificazione o altre tecniche, si
veda il corner detector id Harris:

http://www.dei.unipd.it/~masiero/files/teaching/harris_corner_detector.pdf

I Landmark sono punti di un soggetto aventi una semantica ben nota, dato
un soggetto i landmark da utilizzare devono essere scelti attentamente,
così da poterne garantire la visibilità e identificabilità nelle immagini
del soggetto stesso. Una volta identificati i landmark sono in numero e
ordinamento fisso, così che ogni forma manualmente o automaticamente
identificata in una immagine possa essere manipolata in automatico
lavorando sulla geometria della forma stessa.

Rappresentazione di forma
Coordinate di Bookstein
Coordinate di Kendall
Full Procrustes fit
Altri risultati della Procrustes analysis

Rappresentazione di forma

La rappresentazione di una forma descritta da un numero fisso di
landmark dalla semantica nota può avvenire in differenti modi,
dipendentemente dalle operazioni che si intendono svolgere su di essa e
dalla dimensionalità della forma.

La rappresentazione più intuitiva di una forma è rappresentata da una
matrice le cui colonne contengono le coordinate dei punti (uno per
colonna). Nel caso spcifico di una forma bidimensionale una
rappresentazione spesso più comoda e conveniente consiste in un vettore
colonna a valori complessi, in cui ogni valore complesso z = x + iy
rappresenta un punto della forma.

Indipendentemente da come le coordinate dei landmark siano memorizzate,
differenti rappresentazioni di una forma sono possibili, cominciamo a
definirla:

Una forma è ciò che resta di una struttura geometrica una volta che
vengono eliminate le informazioni di traslazione, rotazione e scala.

Solo nel caso bidimensionale, utilizzando la rappresentazione di forma
come vettore complesso, è possibile definire le operazione di
traslazione, scalatura e rotazione come segue:

W_t = W + (dx + i dy)
W_s = W s
W_r = W e(i\theta)

% Creiamo dei quadrati e rappresentiamoli come coordinate complesse:
csq = pcru2dshape2complex([-1,-1;1,-1;1,1;-1,1]');

% Generiamo dei quadrati con rumore:
nsq = 300; noise = 0.1;
W = noise*rand(size(csq,1),nsq) + 1i*noise*rand(size(csq,1),nsq) + repmat(csq,[1,nsq]);

% Rotazione moltiplicando per un'esponenziale complessa:
W = W.*repmat((10*rand(1,nsq).*exp(1i*2*pi*rand(1,nsq))),[size(csq,1),1]);

% Scalatura moltiplicando per scalari reali:
W = W.*repmat(rand(1,size(W,2))+0.5,[size(W,1),1]);

% Traslazione aggiungendo coordinate complesse:
W = W + repmat(100*((rand([1,size(W,2)])-0.5)+1i*(rand([1,size(W,2)])-0.5)),[size(W,1),1]);

% Vediamoli:
figure; hold on; for i=1:size(W,2); plotshape(pcru2dcomplex2shape(W(:,i))); end

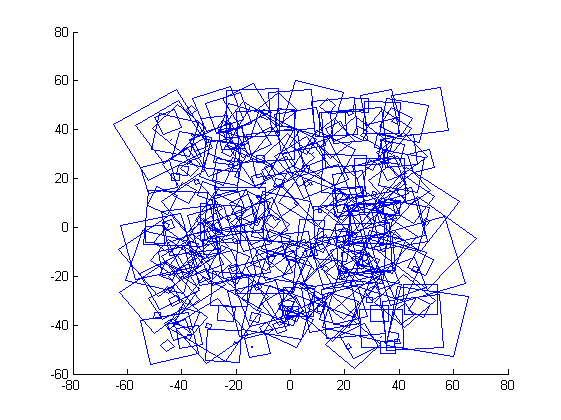
Coordinate di Bookstein

Diverse rappresentazioni di forma sono state definite differente in
letteratura, ad esempio quella di Bookstein o di Kendall.
Bookstein elimina la trasformazione di similarità portando i primi due
landmark in (0;0) e (0;1):

Passiamo alle coordinate di Bookstein (in una cella di matrici-forma):
si osservi che in questa implementazione, per una questione di simmetria,
vengono utilizzati i punti (0,-0.5) e (0,0.5) per l'allineamento dei
primi due landmark (il che ovviamente non modifica le proprietà delle
coordinate di Bookstein).

% Inizializzazione:
Wb = cell(1,size(W,2));
figure; hold on;

% Conversione e visualizzazione:
for i=1:numel(Wb)
    Wb{i} = pcru2dbookstein(pcru2dcomplex2shape(W(:,i)));
    plotshape(Wb{i},true,'r.');
end
axis equal;

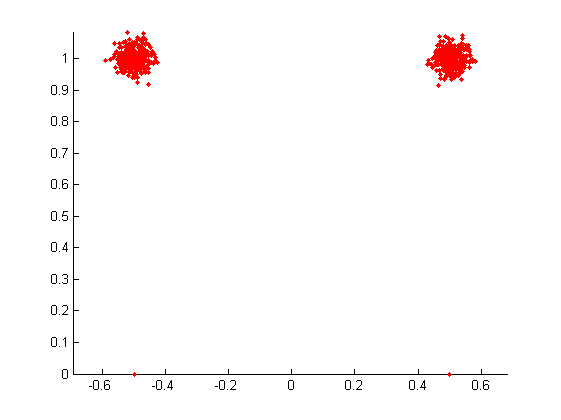
Coordinate di Kendall

Una ulteriore rappresentazione per le forme è ottenibile comodamente
utilizzando le coordinate complesse e le matrici di Helmert. Una matrice
di Helmert per uno spazio vettoriale a d dimensioni consiste in una
matrice ortonormale (quindi una base ortonormale) di cui il primo
versore rappresenta la bisettrive degli assi con tutte le coordinate
equivalenti a 1/sqrt(d), e ogni altro versore coinvolgente il numero
minimo di coordinate (2, 3, ..., d). La j-esima riga di questa matrice,
oltre la prima, assume la seguente forma:

h_j = \overbrace{-\frac{1}{\sqrt{j(j-1)}};\dots}^{j-1\ volte}; \frac{j-1}{\sqrt{j(j-1)}} \overbrace{0; \dots}^{d-j\ volte}

Per k=3 ad esempio si ha:

H_3 = \begin{pmatrix}
         1/\sqrt{3} & 1/\sqrt{3} & 1/\sqrt{3} \\
         -1/\sqrt{2} & 1/\sqrt{2} & 0 \\
         -1/\sqrt{6} & -1/\sqrt{6} & 2/\sqrt{6} \\
      \end{pmatrix}

% Conversione e visualizzazione:
Wk = pcru2dkendall(W);
figure; hold on;
for i=1:size(Wk,2); plotshape(pcru2dcomplex2shape(Wk(:,i)),true,'r.'); end
axis equal;

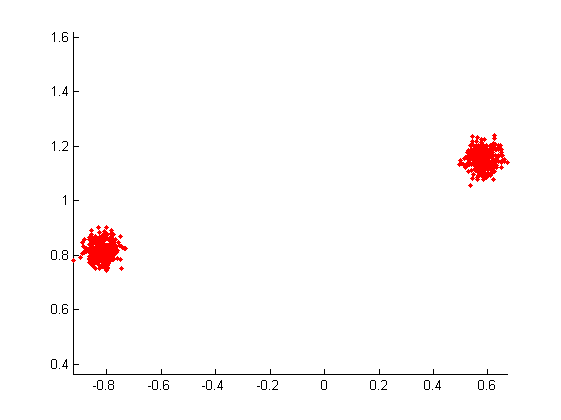
E' possibile mostrare che le coordinate di Bookstein e di Kendall sono facilmente trasformabili le une nelle altre tramite la sottomatrice quadrata a N-2 righe/colonne della matice di Helmert:

W_k = \sqrt{2} H_l W_b

e viceversa:

W_b = \frac{1}{\sqrt{2}}H_l^{-1} W_k

% Matrice di Helmert per forme a 4 landmark e sua sottomatrice:
H = pcruhelmert(4);
Hl = H(3:end,3:end);

% Passaggio da Kendall a Bookstein:
Wb2 = pcru2dcomplex2shape((Hl\Wk(:,1))/sqrt(2));

% Passaggio da Bookstein a Kendall:
Wk2 = sqrt(2)*Hl*pcru2dshape2complex(Wb{1}(:,3:end));

% Vediamo gli errori:
fprintf('Errore massimo K->B: %f\n', max(max(abs(Wb2 - Wb{1}(:,3:end)))));
fprintf('Errore massimo B->K: %f\n', max(max(abs(Wk(:,1) - Wk2))));

Errore massimo K->B: 0.000000
Errore massimo B->K: 0.000000

Full Procrustes fit

Si considerino una forma W, e una forma Y ottenuta per similarità dalla
precendente più una componente di rumore additivo:

Y = W\beta e^{i\theta} + (a + ib)1_k + \epsilon

dove a + ib rappresenta la traslazione, \beta il fattore di scala e \theta l'angolo di rotazione. Convenientemente è possibile "impacchettare" la trasformazione in un vettore complesso 2x1 come segue:

Y = X A + \epsilon = (1_k,W) \begin{pmatrix}a + ib \\ e^{i\theta}\end{pmatrix} + \epsilon

da cui l'allineamento delle due forme W e Y consiste nella determinazione del vettore complesso A contenente i parametri di trasformazione similare tali che l'errore \epsilon^H\epsilon sia minimo, dove ^H rappresenta l'ermitiana di una matrice, ovvero A^H = \overline{A^T}. Si ha:

\hat{A} = \arg\min_A \epsilon^H\epsilon = \arg\min_A (Y-(1_k,W)A)^H(Y-(1_k,W)A)

Sotto l'ipotesi che Y e W siano centrate (centroide nullo), si dimostra
che a=b=0 (essendo Y e W già centrate), inoltre:

\beta e^{i\theta} = \frac{W^HY}{W^HW}

e quindi la forma allineata si ottiene come:

\hat{W} = \frac{W^HYW}{W^HW}

equazione di trasformazione asimmetrica, sotto l'ulteriore ipotesi di normalizzazione W^HW = Y^HY = 1 si ottengono gli allineamenti:

\hat{W} = W^HYW
\hat{Y} = Y^HWY

% Centriamo tutte le forme:
Wc = W - repmat(mean(W,1),[size(W,1),1]);

% Normaliziamole:
Wcn = Wc./repmat(sqrt(sum(conj(Wc).*Wc,1)),[size(Wc,1),1]);

% Allineiamo la rotazione sulla prima forma:
Yr = repmat(Wcn(:,1),[1,size(Wcn,2)-1]);
Wcnr = [Wcn(:,1),repmat(sum(conj(Wcn(:,2:end)).*Yr,1),[size(Wcn,1),1]).*Wcn(:,2:end)];

% Vediamo:
figure;
subplot(121); hold on;
for i=1:size(Wcn,2); plotshape(pcru2dcomplex2shape(Wcn(:,i))); end
axis equal; title('Forme normalizzate');
subplot(122); hold on;
for i=1:size(Wcnr,2); plotshape(pcru2dcomplex2shape(Wcnr(:,i))); end
axis equal; title('Forme allineate');

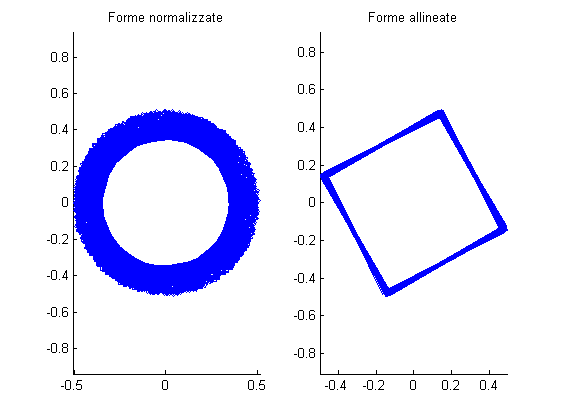
Una misura di distanza tra forme è definita dal valore ottenuto dalla
minimizzazione, ovvero:

\epsilon^H\epsilon = \min_A (Y-(1_k,W)A)^H(Y-(1_k,W)A)

da cui sostituendo la soluzione per A si ottiene:

d(Y,W) = \sqrt{1 - \frac{Y^HW W^HY}{Y^HY W^HW}}

% Le forme sono già tutte normalizzate, calcolo le distanze dalla prima:
Y = repmat(Wcnr(:,1),[1,size(Wcnr,2)]);
dists = sqrt(1 - sum(conj(Y).*Wcnr,1).*sum(conj(Wcnr).*Y,1));

% Scegliamo la forma più distante dalla prima:
[val,pos] = max(dists);

% Vediamole come istogramma:
figure;
subplot(121); hist(dists); title('Istogramma delle distanze tra forme');
subplot(122); hold on;
plotshape(pcru2dcomplex2shape(Wcnr(:,1)));
plotshape(pcru2dcomplex2shape(Wcnr(:,pos)),true,'r');
axis equal; title('Prima forma e forma più distante da essa');

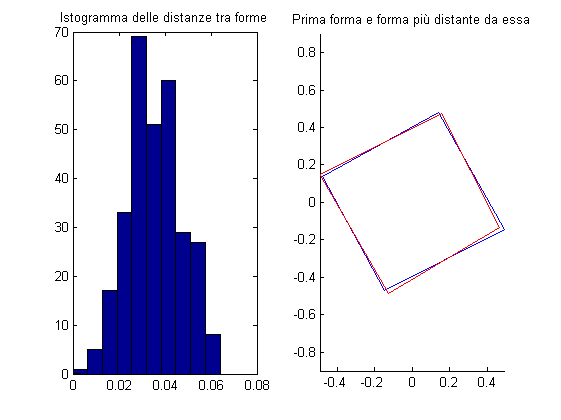
Altri risultati della Procrustes analysis

Altri strumenti sono messi a disposizione dalla Procrustes analysis, in
particolare strumenti di calcolo della scala, della distanza tra forme
(altre distanze diverse dalla full procrustes) della forma media, della
"preforma"... in dsitools esistono alcune funzioni con prefisso "pcru"
che implementano alcuni degli algoritmi descritti dalla procrustes
analysis. Si osservi che alcuni algoritmi e alcune rappresentazioni sono
state descritte in letteratura appositamente per il 2d (in dsitools
prefisso "pcru2d") mentre altre sono generali e applicabili in spazi a
dimensionalità arbitraria (ad esempio a forme geometriche
tridimensionali).

In questa "puntata" non approfondiremo ulteriormente l'argomento essendo
di nostro interesse il solo allineamento di forme 2d, un libro di
riferimento è "Statistical Shape Analysis", Dryden e Mardia, Wiley.