Geometria proiettiva 2D (cenni)

In questo "capitolo" parleremo di geometria proiettiva di base sul
piano, in particolare tratteremo le relazioni che legano tra loro punti,
rette e coniche.

Il piano euclideo offre sicuramente un "ambiente" intuitivo in cui
operare con entità geometriche, come da geometria analitica, in cui però
alcune "simmetrie tra teoremi" sono assenti, ad esempio:

1) Ogni coppia di rette ha un punto di intersezione TRANNE nel caso
   particolare di rette parallele.
2) Ogni retta può essere rappresentata dalla coppia (m,q) nell'equazione
   y = m x + q TRANNE le rette verticali. In questo caso le coordinate
   polari possono aiutare.. ma prevedono l'utilizzo di funzioni
   trascendenti (trigonometriche).
3) Ogni coppia di punti non coincidenti descrive una retta, ma non ogni
   coppia di rette descrive un punto.
4) Scala anisotropa, rotazione e skew (shear) sono trasformazioni
   lineari, MA NON LO E' la traslazione.
    (http://www.wolframalpha.com/input/?i=vertical+shear+45+degrees)

Questi sono esempi di "problemi" che si incontrano nel piano euclideo e
che vogliamo "risolvere" passando al piano proiettivo.

Rappresentazione di rette e punti
Punto da due rette, retta da due punti
Linea all'infinito
Trasformazioni lineari
Coniche

Rappresentazione di rette e punti

In geometria proiettiva 2D punti e rette sono entità duali, in
particolare una retta viene rappresentata in forma omogenea dalla
seguente equazione:

a x + b y + c = 0

Notare che i coefficienti (a,b,c) possono essere scalati arbitrariamente
senza che la retta cambi (purché la scala k non sia nulla):

a x + b y + c = 0 \Leftrightarrow k a x + k b y + k c = 0

Se chiamiamo l = (a,b,c)^T e p = (x,y,1)^T allora l'equazione precedente
dice che un punto p sta sulla retta l sse l^T p = 0. Chiaramente:

l^T p = 0 \Leftrightarrow l^T (k p) = 0

Quindi una retta 2D verrà rappresentata da un vettore a 3 componenti
invariante per scala (2 gradi di libertà), un punto equivalentemente
verrà rappresentato con 3 componenti e si ha:

p = (x_1,x_2,x_3)^T \Rightarrow p_{euclideo} = \left(\frac{x_1}{x_3},\frac{x_2}{x_3}\right)

Punto da due rette, retta da due punti

Indichiamo con \cdot il prodotto interno, e con \times il prodotto
vettoriale (cross) definito come il seguente determinante simbolico:

l' \times l = \left|\begin{matrix} i & j & k \\ l'_1 & l'_2 & l'_3 \\ l_1 & l_2 & l_3 \end{matrix}\right| = \left(\begin{matrix} l'_2 l_3 - l_2 l'_3 \\ l'_3 l_1 - l_3 l'_1 \\ l'_1 l_2 - l_1 l'_2 \end{matrix}\right)

e rappresenta un vettore normale a l' e l con norma uguale all'area del parallelogramma definito da l' e l sul piano su cui giacciono.

Da questo ultimo fatto è chiaro che il seguente prodotto triplo si
annulli essendo proiezione tra vettori ortogonali:

l \cdot l' \times l

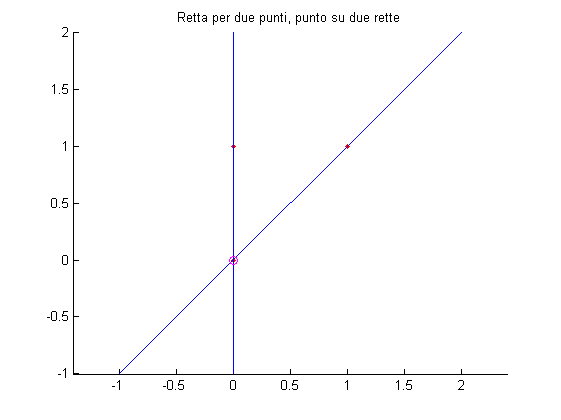
Nel piano proiettivo due rette hanno sempre una intersezione, per
calcolare l'intersezione tra due rette l e l notiamo che il punto di
interesse p deve rispettare le equazioni omogenee:

l \cdot p = 0
l' \cdot p = 0

inoltre notando che:

l \cdot (l' \times l)
l' \cdot (l' \times l)

concludiamo che:

p = l' \times l

Analogamente la retta passante per due punti si ottiene come:

l = p' \times p

% Tre punti:
p1 = [1;1;1]; p2 = [0;0;1]; p3 = [0;1;1];

% Rette tra i primi due e i secondi due:
l12 = cross(p1,p2);
l23 = cross(p2,p3);

% Intersezione dovrebbe essere il punto p2:
p2bis = cross(l12,l23);

% Vediamo:
figure; hold on;
plotpoints([p1,p2,p3],'r.');
plotlines([l12,l23],[-1,2;-1,2],'b');
plotpoints(p2bis,'mo');
axis equal; title('Retta per due punti, punto su due rette');

Linea all'infinito

Rette parallele hanno i primi due coefficienti a e b identici a meno di
un fattore di scala (il rapporto a:b è lo stesso), quindi rette parallele
possono essere scritte come l=(a,b,c)^T e l'=(a,b,c')^T, la loro
intersezione diviene:

l \times l' = (b (c - c'),(c' - c) a,0)^T

punto in coordinate omogenee con la terza coordinata nulla, ovviamente non è possibile mappare questo punto sul piano euclideo (otterremmo delle divisioni per zero), in compenso possiamo interpretare questi punti come punti all'infinito. Tutti i punti del tipo (x_1,x_2,0) formano una retta particolare: la retta all'infinito. Ogni singolo punto può essere inteso come una direzione (data dal vettore formato dalle sole prime due coordinate), in particolare la direzione delle rette di cui è intersezinoe (le infinite parallele lungo quella direzione).

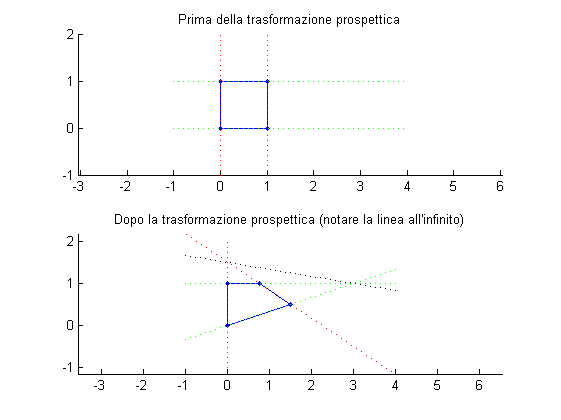
La retta all'infinito non è visibile nel piano euclideo, ma con
opportune trasformazioni prospettiche può essere spostata in maniera da
divenire visibile.

Trasformazioni lineari

Si consideri un punti p = (x,y,1)^T e un vettore traslazione
v = (v_x,v_y)^T), il punto p traslato tramite v è:

p + v = \begin{pmatrix} x + v_x \\ y + v_y \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & v_x \\ 0 & 1 & v_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = T(v) p

La rotazione e la scalatura sono a loro volta trasformazioni lineari
anche nel piano euclideo, orlando la matrice 2x2 che le prappresenta con
zeri (un uno solo sull'ultimo coefficiente in basso a destra) se ne
ottengono le versioni omogenee. Una trasformazione ottenuta componendo
solo rotazione e traslazione è detta rigida, se anche la scalatura
isotropa viene inclusa si parla di similarità.

Una trasformazione arbitraria del tipo:

T = \begin{pmatrix} a&b&c\\d&f&g\\0&0&1 \end{pmatrix}

ha 6 gradi di libertà (2 per la traslazione, 2 per la scala anisotropa, 1 per la rotazione e 1 per lo skew) e prende il nome di affinità. Una trasformazione affine mantiene il parallelismo e la collinearità, non mantiene l'ortogonalità (mantenuta dalle similarità in su). Una matrice 3x3 arbitraria (non singolare) rappresenta una trasformazione prospettica e ha 8 gradi di libertà, i due gradi aggiunti spostano la linea all'infinito che diviene quindi visibile.

Si osservi che una linea l passante per p una volta trasformata passerà
per la versione trasformata di p, ovvero:

\hat{p} = T p
l^T p = 0
\hat{l}^T \hat{p} = \hat{l}^T T p = 0

vero se e solo se:

\hat{l} = T^{-T} l

% Un quadrato:
quad = [0,0;0,1;1,1;1,0]';

% Due rette relative a due lati paralleli:
l1 = linesfrom2points(quad(:,1),quad(:,2));
l2 = linesfrom2points(quad(:,3),quad(:,4));
l3 = linesfrom2points(quad(:,1),quad(:,4));
l4 = linesfrom2points(quad(:,2),quad(:,3));

% Una trasformazione prospettica:
T = [3,0,0;1,3,0;1,2,1];

% Quadrato trasformato:
quadT = T*points2domogenize(quad);

% Rette trasformate:
l1T = inv(T)'*l1;
l2T = inv(T)'*l2;
l3T = inv(T)'*l3;
l4T = inv(T)'*l4;

% Linea all'infinito trasformata:
linf = [0;0;1];
linfT = inv(T)'*linf;

% Vediamo:
clipping = [-1,4;-1,2];
figure;
subplot(211); hold on;
plotshape(quad,true,'b.-');
plotlines([l1,l2],clipping,'r:');
plotlines([l3,l4],clipping,'g:');
axis equal; title('Prima della trasformazione prospettica');
subplot(212); hold on;
plotshape(quadT,true,'b.-');
plotlines([l1T,l2T],clipping,'r:');
plotlines([l3T,l4T],clipping,'g:');
plotlines(linfT,clipping,'k:');
axis equal; title('Dopo la trasformazione prospettica (notare la linea all''infinito)');

Coniche

Una conica è definita come il luogo geometrico del piano che verifica la
seguente equazione omogenea:

a x^2 + b x y + c y^2 + d x + e y + f = 0

anche scrivibile come segue:

\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}^T \begin{pmatrix} a & b/2 & c/2 \\ b/2 & d & e/2 \\ c/2 & e/2 & f \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = p^T C p = 0

quindi una conica può essere rappresentata come una matrice simmetrica 3x3, e un punto p si trova su una conica C se la forma quadratica p^T C p si annulla. Come per i casi precedenti l'equazione è omogenea, quindi le coniche C e k C per ogni scala non nulla k sono identiche.

Varie proprietà delle coniche divengono utili se non indispensabili
nella computer vision, in particolare grazie alla relazione tra le
coniche e il modello di acquisizione di immagini "pin-hole camera".

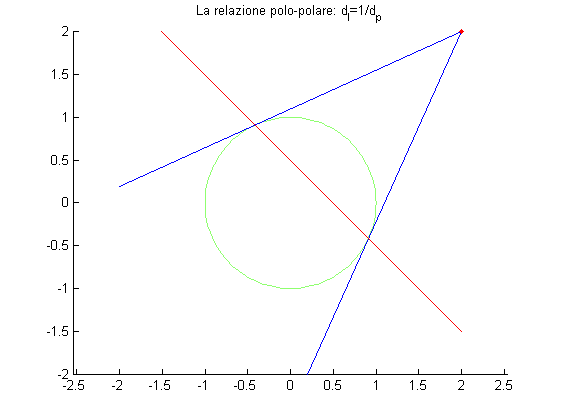
Una circonferenza centrata è descritta da un'equazione del tipo:

x^2 + y^2 - r^2 = 0

ovvero è rappresentata dalla matrice:

\begin{pmatrix} 1&0&0\\0&1&0\\0&0&-r^2 \end{pmatrix}