Valutazione di un classificatore

Considerata l'impossibilità di costruire un classificatore universale
migliore in assoluto, dovendo quindi valutare per ogni problema quale
tecnica risulti migliore, sorge il problema di poter valutare la bontà di
un classificatore applicato a un dato problema di classificazione. Si
osservi che per la valutazione di un classificatore l'unico strumento
utilizzabile è il classificatore stesso ed il dataset di addestramento.

Valutazione di un singolo test
K-Folding

Valutazione di un singolo test

Per la valutazione delle performance di un classificatore devono essere
seguite le fasi di addestramento e test su dataset differenti, per questo
motivo il dataset di addestramento viene suddiviso in due parti, una
delle quali viene utilizzata per l'addestramento e l'altra per il test.

La valutazione della bontà di un classificatore avviene calcolando
alcuni coefficienti tra cui:

Accuratezza:     Percentuale di classificazioni corrette.
Precision:       Percentuale di positivi trovati.
Recall:          Percentuale di documenti trovati.

Per il calcolo di queste misure spesso si ricorre all'utilizzo di:

TP:      Numero di veri positivi (classificati true erano true).
TN:      Numero di veri negativi (classificati false erano false).
FP:      Numero di falsi positivi (classificati true anche se false).
FN:      Numero di falsi negativi (classificati false anche se true).

da cui:

accuracy = \frac{TP+TN}{TP+TN+FP+FN}
precision = \frac{TP}{TP+FP}
recall = \frac{TP}{TP+FN}

% Carico il dataset:
load mnist_01r2;

% Preparo i dati di train:
samples = double([train0,train1]);
classification = [false(1,size(train0,2)),true(1,size(train1,2))];

% Addestro un classificatore:
net = OIPCAClearn(samples,classification);

% Preparo il dataset di test:
testSamples = double([test0,test1]);
testClassification = [false(1,size(test0,2)),true(1,size(test1,2))];

% Eseguo il test:
sclass = OIPCACclassify(net,testSamples);

% Calcolo l'accuratezza:
acc = sum(sclass==testClassification)/numel(sclass);

% Calcolo TP, TN, FP, FN:
TP = sclass & testClassification;
TN = not(sclass) & not(testClassification);
FP = sclass & not(testClassification);
FN = not(sclass) & testClassification;

% Precision e recall:
precision = TP/(TP+FP);
recall = TP/(TP+FN);

% Vediamo i risultati:
fprintf('accuracy: %2.2f%%\nprecision: %2.2f%%\nrecall: %2.2f%%\n',acc*100,precision*100,recall*100);

accuracy: 99.81%
precision: 99.91%
recall: 99.74%

K-Folding

Una valutazione più accurata di un classificatore può essere ottenuta
iterando la procedura seguente sull'intero dataset operando come segue:

1) fissato un valore intero K>1, il dataset viene partizionato;
2) ad ogni iterazione K-1 parti vengono usate per l'addestramento e una
   per il test;
3) le misure di bontà del classificatore vengono mediate.

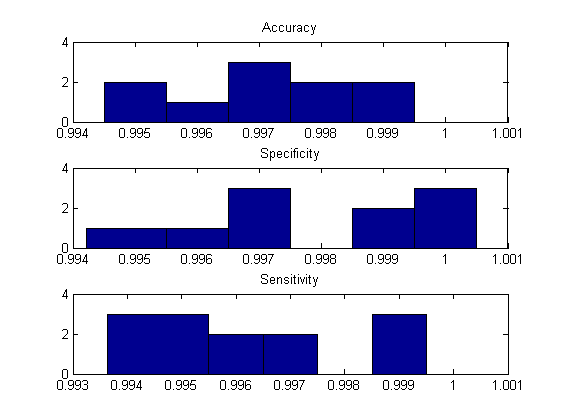
Se si utilizza K=N numero totale di esempi si ottiene leave-one-out, ad
ogni iterazione tutto il dataset tranne un elemento viene utilizzato per
l'addestramento e un solo esempio viene usato per il test, l'insieme
finale di classificazioni viene usato per il calcolo delle misure di
bontà del classificatore.

Altre misure spesso utilizzate sono:

Specificity:     Abilità nell'identificare i negativi.
                 specificity = \frac{TN}{TN+FP}
Sensitivity:     Abilità nell'identificare i positivi.
                 specificity = \frac{TP}{TP+FN}

%  Preparo i dati:
samples = [samples,testSamples];
classification = [classification,testClassification];

% Esecuzione del K-Folding:
[accuracies,specificity,sensitivity] = ...
    KFolding(samples,classification,'OIPCAC',{},10);

% Vediamo i risultati:
figure; Hx = 0.995:0.001:1;
subplot(311); hist(accuracies,Hx); title('Accuracy');
subplot(312); hist(specificity,Hx); title('Specificity');
subplot(313); hist(sensitivity,Hx); title('Sensitivity');

Valutazione di un classificatore

Contents

Valutazione di un singolo test

K-Folding