Classificazione binaria

In questo "capitolo" verranno descritte le problematiche di
classificazione automatica e alcune possibili soluzioni proposte
nell'ambito dell'apprendimento automatico supervisionato.

Scopo dell'apprendimento automatico supervisionato è quello di "imparare
a discrimintare" a partire da esempi di entità già discriminate. In
particolare, siano \bar{X}=\{\bar{x}_i\}_{i=1}^N dei vettori di
caratteristiche estratte da soggetti di interesse (ad esempio patch di
immagini contenenti i soggetti da discriminare). Si immagini inoltre di
avere a disposizione le classificazioni di ogni vettore x_i come
appartenente alla classe di oggetti A oppure B (ad esempio faccia e
non-faccia), identificata da un vettore \bar{Y} = \{\bar{y}_i\}_{i=1}^N
di valori 0 (classe A) e 1 (classe B). Scopo è stimare la funzione
f: \Re^d\to\{0,1\} capace, dato un nuovo vettore di caratteristiche, di
classificarlo come appartenente alla classe A (0) o B (1).

Un classificatore con apprendimento automatico è quindi una funzione
del seguente tipo:

f: R^d\times\left(R^d\times\{0,1\}\right)^N \to \{0,1\}

In particolare il miglior classificatore è quello che commette ha
probabilità minima di commettere errori:

f^* = \arg\min_f P\left(f(x)\neq y|\{(x_i,y_i)\}_{i=1}^N\right)

Si dimostra che, se nota la distribuzione \eta(x)=P(y=1|x), allora il
miglior classificatore diviene il seguente:

f^*(x) = \left\{ \begin{matrix} 1 \hfill\quad\text{\ se\ }\eta(x)>0.5 \\ 0 \hfill\quad\text{\ altrimenti} \end{matrix} \right.

Bayes
KNN
Classificatori lineari
Sottospazio di Fisher
Non-lineare tramite il kernel-trick

Bayes

Si osserivi che data una distribuzione di probabilità bivariata P(x,y),
è possibile scomporla come prodotto di una funzione di probabilità
condizionata per la distribuzione di x: P(x,y) = P(y|x)P(x); risulta vero
anche il viceversa: P(x,y) = P(x|y)P(y).
Eguagliando si ottiene la regola di Bayes:

P(y|x) = \frac{P(x|y)P(y)}{P(x)}

Se si utilizza la stessa semantica della sezione precedente per le
varibili, allora:

f^*(x) = \arg\max_y P(y|x) \\ = \arg\max_y \frac{P(x|y)P(y)}{P(x)} \\ = \arg\max_y P(x|y)P(y)

dove P(y) si chiama prior o probabilità a priori, P(x|y) si chiama likelihood o verosomiglianza, mentre P(y|x) prende il nome di posterior, o probabilità a posteriori. Detto questo, il miglior classificatore (chiamato classificatore di Bayes data la sua origine) prende anche il nome di maximum a posteriori (MAP).

Nota: in spazi ad elevata dimensionalità (con un numero sufficiente alto
di caratteristiche nei vettori x) la stima di P(y|x) dai dati di
addestramento \{(x_i,y_i)\}_{i=1}^N risulta di difficile applicazione
senza ipotesi ulteriori.

Vediamo un esempio di stima di P(y|x) basata su Parzen, ovvero stimiamo
la distribuzione di probabilità utilizzando una funzione k (detta kernel)
come modello base di probabilità in ogni intorno, la combinazione lineare
di tale funzione traslata in tutti i punti di training fornisce la stima
della funzione di probabilità:

P(x|y=1) \approx \frac{1}{Z_1}\sum_{i=1}^N y_i k(x|x_i,\sigma)
P(x|y=0) \approx \frac{1}{Z_0}\sum_{i=1}^N (1-y_i) k(x|x_i,\sigma)

con Z_* fattore di normalizzazione, \sigma parametro.

Vediamo un esempio di classificatore MAP ottenuto utilizzando Parzen per
modellare le likelihood functions.
NOTA: si osservi che un classificatore costruito come segue prevede di
mantenere a tempo di classificazione tutti i dati di addestramento, il
che in certi casi è assolutamente inapplicabile.

% Genero dati da due gaussiane (training set):
g = @(mu,sigma,N)(randn(2,N)*sigma+repmat(mu,[1,N]));
ptsA = g([40;20],3,1000);
ptsB = g([10;40],2,500);
X = [ptsA,ptsB];
Y = [zeros(1,size(ptsA,2)),ones(1,size(ptsB,2))];

% Le prior:
P_y0 = size(ptsA,2)/(size(ptsA,2)+size(ptsB,2));
P_y1 = size(ptsB,2)/(size(ptsA,2)+size(ptsB,2));

% Il kernel (Gaussiano RBF):
Norm = @(X)(sqrt(sum(X.^2,1)));
sigma = 1;
k = @(X,x_i)(gauss(Norm(X-repmat(x_i,[1,size(X,2)])),sigma));

% Stima delle PDF:
[X1,X2] = meshgrid(1:50);
pts = [X1(:),X2(:)]';
P_y0x = zeros(size(X1));
P_y1x = zeros(size(X1));
for i=1:size(X,2)
    kvals = reshape(k(pts,X(:,i)),size(P_y0x));
    P_y0x = P_y0x + (1-Y(i))*kvals;
    P_y1x = P_y1x + Y(i)*kvals;
end
P_y0x = P_y0x/size(ptsA,2);
P_y1x = P_y1x/size(ptsB,2);

% Vediamoli:
figure;
subplot(121);
imshow(cat(3,imscale(P_y0x),zeros(size(P_y0x)),imscale(P_y1x)));
title('Le due likelihood functions');
subplot(122);
imshow(P_y0x*P_y0 < P_y1x*P_y1); hold on; plotpoints(ptsA,'r.'); plotpoints(ptsB,'b.');
title('Classificazione MAP');

KNN

Un altro metodo per classificare dati i dati di addestramento consiste
nel, dato un punto nuovo, cercarne il più vicino utilizzando una nozione
di distanza, ad esempio la distanza euclidea; in questo caso si parla di
Nearest Neighbor Classifier. Un simile classificatore gode di varie
proprietà, tra cui la capacità di essere esteso al caso multi-classe in
maniera semplice e naturale. Per contro, anche NN prevede il mantenimento
dei dati a tempo di classificazione, inoltre risulta sensibile alla
presenza di outlier, ovvero di dati di addestramento generati in regioni
a bassa probabilità.

Un classificatore consistente è un classificatore f tale per cui:

\lim_{N\to+\infty} f = f^*

ovvero che converge verso il classificatore i Bayes (ottimo). Il classificatore NN non è un classificatore consistente, è però possibile estenderlo affinché lo sia: si fissi un parametro intero positivo k > 0, dato un nuovo punto x si determinino i k punti di addestramento \hat{X} più vicini a x con etichette \hat{Y}, se \sum_{y\in\hat{Y}} y > 0.5|\hat{Y}| allora viene assegnata la classe 1, ovvero se la maggioranza dei punti di training trovati è di classe 1 viene assegnata quella classe; questo classificatore viene chiamato KNN. Si dimostra che KNN è un classificatore consistente a patto di far crescere k al crescere di N garantendo che:

N \to +\infty, k \to +\infty, k/N \to 0^+

% Classifichiamo:
k = 3;
knnclass = knnclassify(pts',X',Y,k);

% Vediamo il risultato:
figure;
imshow(reshape(knnclass,size(X1))); hold on; plotpoints(ptsA,'r.'); plotpoints(ptsB,'b.');
title('Classificazione KNN');

Classificatori lineari

Una caratteristica importante per quelunque classificatore è la sua
complessità computazionale (tempo e spazio) in fase di classificazione,
dopo che la fase di addestramento si è conclusa, questo perché spesso
l'addestramento avviene una sola volta off-line, mentre la
classificazione avviene durante l'utilizzo vero e proprio dello
strumento, si consideri ad esempio le applicazioni embedded (videocamere
intelligenti, fotocamere digitali, ...). Al fine di poter costruire
classificatori efficienti è indispensabile identificare un modello
parametrico i cui parametri (meno possibile) vengono stimati a tempo di
addestramento e mantenuti a tempo di classificazione. Il modello può
riguardare ad esempio le distribuzioni di probabilità, oppure la
superficie di separazione (curve negli esempi precedenti). In
particolare se il modello descrive la superficie di separazione tramite
un iperpiano, allora si parla di classificatori lineari. Si consideri la
segiente equazione di un iperpiano in \Re^d:

w_1 x_1 + w_2 x_2 + \dots + w_d x_d - \gamma = w x - \gamma = 0

dove w + un vettore riga contenente i coefficienti w_1 \dots w_n, mentre \gamma viene detto termine noto, questa rappresentazinoe di piano si dice omogenea. La regola di classificazione derivante da questo modello di iperpiano separatore diviene semplicemente:

w x > \gamma

La stima del vettore w e della soglia \gamma è lo scopo degli algoritmi
di addestramento di classificatori lineari.

% Un esempio costruito "a mano":
w = [-2,1.5];
gamma = 0;

% Vediamo il risultato:
figure;
imshow(X1*w(1)+X2*w(2)>gamma); hold on; plotpoints(ptsA,'r.'); plotpoints(ptsB,'b.');
title('Classificazione lineare');

Sottospazio di Fisher

La disequazione w x > \gamma proietta i punti in un sottospazio
mono-dimensinoale identificato dal vettore w e li discrimina in base ad
una soglia:

% Proiettiamo i punti e vediamone la distribuzione:
absc = -80:10:60;
HA = hist(w*ptsA,absc);
HB = hist(w*ptsB,absc);
figure; hold on;
bar(absc,HA,'r');
bar(absc,HB,'b');
title('Istogrammi della proiezione sul sottospazio definito da w');

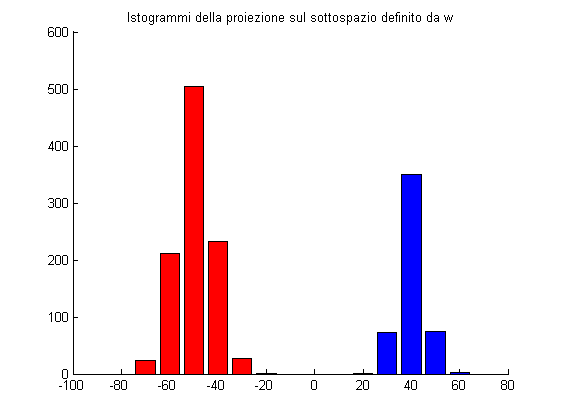
Risuta di fondamentale importanza identificare il sottospazio migliore
in cui proiettare i dati, tale per cui le classi risultino maggiormente
discriminabili. Fisher propose la massimizzazione del seguente criterio:

J(w) = \frac{|\mu_A-\mu_B|^2}{\sigma_A^2+\sigma_B^2}

dove \mu_A e \mu_B sono le medie delle classi, mentre \sigma_A e \sigma_B sono le rispettive deviazioni standard. Nel caso particolare in cui le distribuzioni di probabilità delle due classi siano normali questo criterio risulta ottimo. Si dimostra che nel caso in cui si abbiano due classi descritte da distribuzioni normali omoscendastiche (stessa covarianza, il classificatore ottenuto coincide col classificatore di Bayes. In caso contrario il classificatore risulta sub-ottimale, anche se in pratica fornisce risultati spesso molto buoni.

Resta da capire come stimare w = \arg\min_{\hat{w}} J(\hat{w}). Si
mostra che lo stesso criterio di Fisher può essere espresso come:

J(w) = \frac{\textbf{varianza inter-classe}}{\textbf{varianza intra-classe}}

ovvero:

J(w) = \frac{w(\mu_A-\mu_B)(\mu_A-\mu_B)^Tw^T }{w(\Sigma_A + \Sigma_B)w^T}

In particolare, operando sui punti una trasformazione che rendenda
identica la matrice \Sigma_A + \Sigma_B e forzando w a norma 1, si
ottiene come sottospazio ottimo quello congiungente le medie trasformate.
Si dimostra che tale trasformazione è quella di whitening (sbiancamento
dei dati). Similmente alla PCA, nel whitening si opera la decomposizione
della matrice di covarianza costruendo la trasformazione W come segue:

Xc = \left\{x - \mu | x\in X, \mu=\mathbb{E}\[x\]\right\}
Xc Xc^T = V D V^T
W = D^{-1/2} V^T

Dopo aver applicato la trasformazione W si può ottenere il sottospazio
di Fisher come il sottospazio che spanna le medie trasformate con W:

\bar{w} = W((\mu_A-\mu)-(\mu_B-\mu)) = W(\mu_A-\mu_B)

Il vettore w è quindi ottenuto combinando la trasformazione W dei dati e
la successiva proiezione sul sottospazio di Fisher:

w = \bar{w}^T W = (W(\mu_A-\mu_B))^T W = (\mu_A-\mu_B)^T W^T W \\
  = (\mu_A-\mu_B)^T V D^{-1} V^T = (\mu_A-\mu_B)^T (X X^T)^{-1} \\
  = (\mu_A-\mu_B)^T \Sigma^{-1}

Si osservi che \Sigma^{-1} potrebbe non esistere se la stima della
matrice di covarianza proviene da un numero di campioni inferiore alla
dimensionalità dello spazio (o se sono linearmente dipendenti tra loro).
Varie tecniche sono state proposte in letteratura per la stima del
valore \gamma ottimale.

% % Otteniamo la trasformazione di whitening:
% Xc = X - repmat(mean(X,2),[1,size(X,2)]);
% [V,D] = eig(Xc*Xc');
% W = D^(-1/2)*V;
%
% % Otteniamo il vettore w:
% w = (W*(mean(ptsA,2)-mean(ptsB,2)))'*W;

% Implementazione vanilla:
w = (mean(ptsA,2)-mean(ptsB,2))'/cov(X');

% Proiettiamo e vediamo:
figure;
subplot(121); plotpoints(W*Xc,'r.'); axis equal;
title('Risultato della trasformazione');
subplot(122); imshow(reshape(w*pts<0,size(X1))); hold on; plotpoints(ptsA,'r.'); plotpoints(ptsB,'b.');

Non-lineare tramite il kernel-trick

Alcuni problemi sono risolvibili utilizzando una superificie di
separazione lineare (iperpiano), altri invece sono intrinsecamente non
linari, per questo motivo le tecniche lineari come la precedente non sono
applicabili. Qualunque tecnica lineare che faccia uso esclusivamente del
prodotto interno tra dati di addestramento o con vettori nuovi può essere
trasformata in una tecnica kernel. Una tecnica kernel considera una mappa
\Phi che trasporti i dati in unom spazio a dimensionalità più alta (o
infinita) dove li si ipotizzano linearmente separabili, per poi operare
in quello spazio con il prodotto interno. La mappa \Phi non deve essere
esplicitamente nota né valutata realmente, ciò che in pratica è
indispensabile è una funzione k che calcoli il prodotto interno tra due
punti x_1 e x_2 mappati, ovvero:

k(x_1,x_2) = \left<\Phi(x_1),\Phi(x_2)\right>

Si osservi che k: \Re^d\times\Re^d \to \Re è una funzione che non
coinvolge direttamente la dimensionalità potenzialmente infinita dello
spazio in cui \Phi mappa i punti, cosa che avviene solamente a livello
teorico. In compenso non tutte le funzioni possono essere utilizzate come
funzioni kernel, dato che devono rappresentare un prodotto interno,
le funzioni kernel devono godere delle proprietà seguenti:

1) k(x_1,x_2) = k(x_2,x_1)
2) k(x_1,x_2+x_3) = k(x_1,x_2) + k(x_1,x_3)
3) k(x_1,\alpha x_2) = \alpha k(x_1,x_2)

Il kernel più utilizzato è quello RBF gaussiano:

k(x_1,x_2) = e^{-\frac{\|x_1-x_2\|}{2\sigma^2}}

Si definisce la matrice kernel, o matrice di design (altresì nota come
Gram matrix per il suo significato in geometria differenziale) la
seguente matrice simmetrica definita positiva (e la sua decomposizione):

K = {k(x_i,x_j)}_{i,j=1}^N
K = A \Lambda A^T

Si dimostra che N^{1/2} A rappresenta la proiezione dei punti di
addestramento sulle componenti principali, inoltre il sottospazio di
Fisher nello spazio in cui vengono mappati i punti è spannato dal
seguente vettore normale:

w_{\Phi} = N^{-1/2}(N_AN_B)^{1/2} A^T N_{A|B}

con

N_{A|B} = \left(\underbrace{N_A^{-1}\dots}_{N_A},\underbrace{N_B^{-1}\dots}_{N_B}\right)^T

Si dimostra inoltre che, dato un nuovo punto p e chiamato:

k(p) = \{k(x_i,p)\}_{i=1}^N

il vettore dei prodotti interni di p con tutti gli x_i nello spazio kernel, allora la proiezione di p sul sottospazio di Fisher è:

proj_{Fisher}(p) = k(p)^T w
w = (N_A N_B)^{1/2} A \Lambda^{-1} A^T N_{A|B}^{-1}

con w calcolabile interamente a tempo di addestramento. Si osservi che quanto detto vale le caso in cui i dati siano già cemtrati nello spazio kernel, altrimenti un passaggio di centramento di K deve essere effettuato; chiamando \tilde{K} la versione di K non centrata, il centramento avviene come segue:

K = \tilde{K} - 1_N\tilde{K} - \tilde{K}1_N + 1_N\tilde{K}1_N

con 1_N matrice quadrata NxN contenente tutti N^{-1}.

% Calcolo la matrice di Gram:
K = KernelMatrix(X);

% La decompongo:
[A,Lambda] = eig(K);

% Inverto Lambda in maniera "furba":
LambdaInv = diag(Lambda);
LambdaInv(abs(LambdaInv)<1e-8) = 0;
LambdaInv(LambdaInv~=0) = 1./LambdaInv(LambdaInv~=0);
LambdaInv = diag(LambdaInv);

% Calcolo il vettore w:
N_A = size(ptsA,2); N_B = size(ptsB,2);
N_AB = [repmat(N_A^(-1),[N_A,1]);repmat(N_B^(-1),[N_B,1])];
w = (N_A * N_B)^(1/2) * A * LambdaInv * A' * N_AB.^(-1);

% Proietto sul sottospazio di Fisher:
proj = KernelResponse(pts,X)*w;

% Vediamo:
figure; imshow(reshape(proj<0,size(X1))); hold on; plotpoints(ptsA,'r.'); plotpoints(ptsB,'b.');

Classificazione binaria

Contents

Bayes

KNN

Classificatori lineari

Sottospazio di Fisher

Non-lineare tramite il kernel-trick