Filtri Lineari (per bordi e non) e trasformata di hough

I filtri lineari hanno proprietà matematiche ben definite dalla teoria
dell'elaborazione dei segnali nel dominio delle frequenze, descritti
dalla trasformata di Fourier (nel nostro caso bidimensionale) e

Estrazione dei bordi tramite Sobel
Altri filtri lineari derivativi
Derivata della Gaussiana
Trasformata di Hough

Estrazione dei bordi tramite Sobel

Alcuni pattern possono essere localizzati sfruttandone le proprietà
geometriche, si pensi ad una scacchiera piuttosto che un rettangolo
distorto "solo" dalla prospettiva. Per poter lavorare con la geometria è
indispensabile poter estrarre i bordi dall'immagine, così da poter
identificare delle forme come linee, circonferenze o altro.

% Carico un'immagine contenente un pattern:
img = imtype(imread('coins.png'),'gF');

% Estraggo i bordi con Sobel:
edges = edge(img,'sobel');

% Sovrappongo:
imgEdge = cat(3,min(img,not(edges)),min(img,not(edges)),max(img,edges));
figure; imshow(imgEdge);

Da dove proviene questo risultato? L'algoritmo di Sobel "vanilla" è un
filtro lineare la cui risposta all'impulso è:

            1  2  1
            0  0  0
           -1 -2 -2

per i bordi orizzontali, e:

            1  0 -1
            2  0 -2
            1  0 -1

per quelli verticali. Si osservi che l'integrale della risposta all'impulso è 0 (condizione necessaria per i filtri passa-alto). Applichiamo l'operatore di convoluzione (bidimensioale) all'immagine utilizzando questi due filtri:

% I filtri:
So = fspecial('sobel');
Sv = So';

% Le convoluzioni:
edgeso = filter2(So, img, 'valid');
edgesv = filter2(Sv, img, 'valid');

% Vediamo cosa salta fuori:
figure;
subplot(121); imshowscale(edgeso);
subplot(122); imshowscale(edgesv);

Vediamo i bordi in valore asoluto e scalati:

% Valore assoluto e scalatura tra 0 e 1:
figure;
subplot(121); imshowscale(imscale(abs(edgeso)));
subplot(122); imshowscale(imscale(abs(edgesv)));

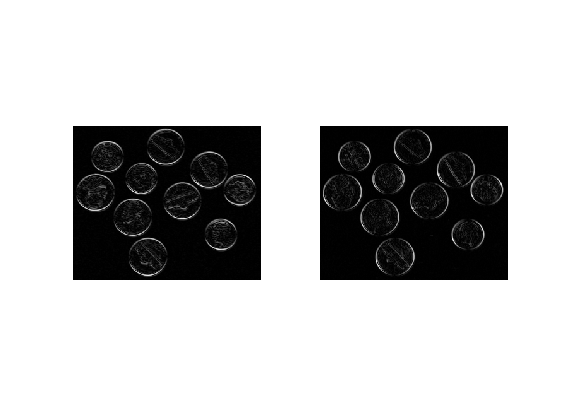
Una sola immagine di bordi la otteniamo calcolando la norma del
gradiente che stiamo approssimando con Sobel:

edges = imscale(sqrt(edgeso.^2 + edgesv.^2));
figure; imshow(edges);

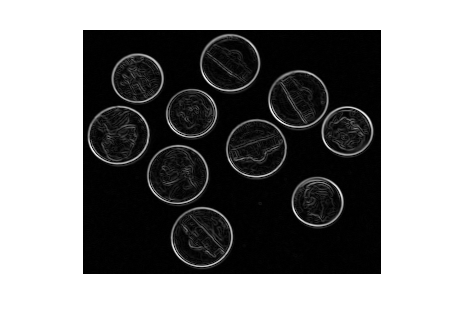
Su questo risultato una sogliatura permette di ottenere i bordi
dell'immagine, si osservi dal risultato che i bordi NON sono definiti da
un solo pixel di larghezza, per ottenere un solo pixel di larghezza
dobbiamo eseguire l'algoritmo morfologico di thinning:

% Sogliatura:
BW = threshold(edges,thresholdValue(edges,'otsu'));

% Il thinning:
BWthinned = bwmorph(BW,'thin',inf);

% Vediamo:
figure;
subplot(121); imshow(BW);
subplot(122); imshow(BWthinned);

Altri filtri lineari derivativi

Problemi con Sobel (Prewit, Roberts): eventuale rumore (ad esempio sale
e pepe) può generare bordi non desiderati, un filtro spesso utilizzato
per attenuare il noise è il filtro Gaussiano.

NOTA: il filtro Gaussiano è un filtro passa-basso, il filtro di Sobel è
un filtro passa-alto, la combinazione dei due è un filto passa-banda. Per
combinare i due filtri è sufficiente moltiplicarne le risposte agli
impulsi nel dominio delle frequenze... oppure convolverli nel dominio
spaziale. Il filtro che otteniamo è una approssimazione del filtro
derivativo Gaussiano.

% Filtro gaussiano:
Gf = fspecial('gauss');

% Filtro risultante (verticale):
Hv = conv2(Gf, Sv);

% Applicazione del filtro:
edgesv = filter2(Hv, img, 'valid');

% Vediamo:
figure;
subplot(131); surf(Sv); axis equal; title(gca, 'Sobel verticale');
subplot(132); surf(Gf); axis equal; title(gca, 'Filtro Gaussiano');
subplot(133); surf(Hv);  axis equal; title(gca, 'Filtro risultante (verticale)');
figure; imshowscale(edgesv);

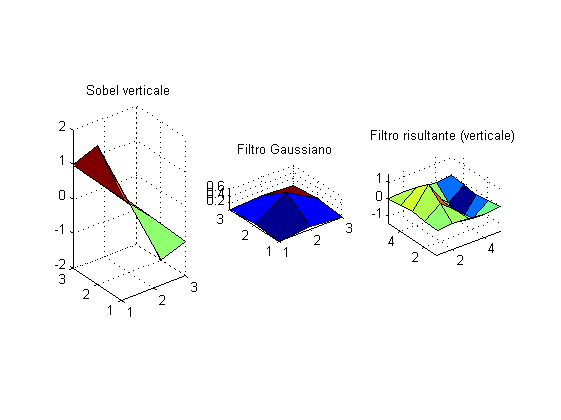
Proviamo anche ad ottenere la composizione dei filtri nelle due
direzioni principali come abbiamo fatto con Sobel:

% Il filtro:
Ho = conv2(Gf, So);

% Applichiamolo:
edgeso = filter2(Ho, img, 'valid');

% Composizione:
gradNorm = sqrt(edgeso.^2 + edgesv.^2);

% Thinning:
edges = bwmorph(threshold(gradNorm,thresholdValue(gradNorm)),'thin',inf);

% Vediamo:
figure;
subplot(121); imshow(gradNorm);
subplot(122); imshow(edges);

Derivata della Gaussiana

La funzione di Gauss è:

g(x,mu,sigma) = exp(-0.5(x-mu)^2/sigma^2);

con massimo in mu di valore g(mu) = 1. Calcolandone la derivata otteniamo un filtro derivativo a una dimensione (consideriamo mu=0):

dg_x = -x/sigma^2 exp(-0.5 x^2/sigma^2)

Utiliziamo dg_x in una direzione e g nell'altra componendo i due filtri
tramite la convoluzione, il risultato è il seguente:

% Le funzioni dei due filtri:
g = @(x,sigma)(exp(-0.5*x.^2./sigma.^2));
dg_x = @(x,sigma)(-x./sigma.^2.*exp(-0.5*x.^2./sigma.^2));

% Calcoliamo due supporti validi per questi filtri:
sigma = 1;
Xvalues = -3*sigma:3*sigma;
Hg = g(Xvalues,sigma);
Hg = Hg / sum(Hg(:));           % Integrale deve dare 1.
Hdg_x = dg_x(Xvalues,sigma);
Hdg_x = Hdg_x - mean(Hdg_x(:)); % Integrale deve dare 0.

% Composizione:
H = conv2(Hg',Hdg_x);

% Applichiamolo:
edgeso = filter2(H, img, 'valid');
figure; imshowscale(abs(edgeso));

Il filtro ottenuto somiglia tanto a Sobel convoluto con Gauss:

figure; surf(H);

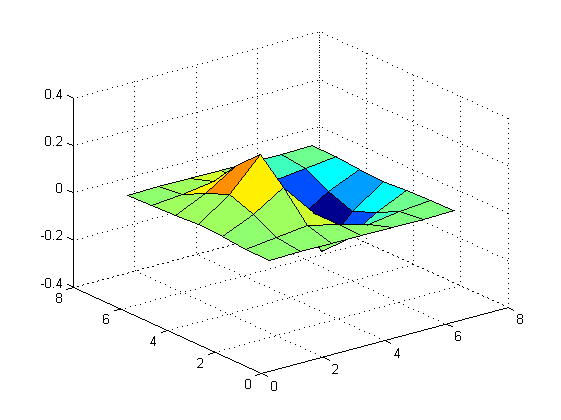
Nulla ci vieta in questo caso di calcolare derivate direzionali, è
infatti sufficiente "pesare" le componenti orizzontale e verticale
dipendentemente dall'angolo:

% 30 gradi:
alpha = 30*pi/180;

% Applico il filtro in entrambe le direzioni:
edgeso = filter2(H, img, 'valid');
edgesv = filter2(H', img, 'valid');

% Ottengo la derivata direzionale:
edgesDir = edgeso*cos(alpha) + edgesv*sin(alpha);
figure; imshowscale(abs(edgesDir));

Trasformata di Hough

Trovati gli edge in questo esempio dobbiamo identificare le
circonferenze delle monete, per farlo utiliziamo la trasformata di Hough
per circonferenze.

Eseguo la trasformata, notare i parametri (non facili da settare):
* ipotizzo di conoscere un valore approssimato di raggio (r=28)
* esiste da settare una soglia (th=30)

% Bordi e trasformata:
[Accumulator,y0detect,x0detect] = houghcircle(edges,28,30);

% Mostro l'accumulatore ed il risultato:
figure;
subplot(121); imshowscale(Accumulator);
subplot(122); imshow(img); hold on; plot(x0detect,y0detect,'ro');

Ma come funziona la trasformata di Hough?

Per ogni punto fornito con gli edge viene prodotto un voto nello spazio
dei parametri, in questo caso il raggio è dato e i parametri rimasti sono
c_x e c_y (coordinate del centro c), ovvero ciò che vediamo nell'immagine
di Accumulator. Il risultato su una immagine BW contenente pochi punti
aiuta a comprendere il meccanismo:

% Creo una immagine apposta:
BW = rand(300) < 0.0001;
Accumulator = houghcircle(BW,28);

% Cosa genera?
figure; imshow(cat(3,max(BW,Accumulator),BW,BW));

NOTA: lo strumento che stiamo utilizzando campiona in maniera errata i
punti su cui generare i voti (si osservino le circonferenze)...
...correggiamolo assieme!

Filtri Lineari (per bordi e non) e trasformata di hough

Contents

Estrazione dei bordi tramite Sobel

Altri filtri lineari derivativi

Derivata della Gaussiana

Trasformata di Hough