Alcuni importanti filtri basati sulla convoluzione
Nella teoria dell'image filtering i filtri lineari hanno una determinante importanza, tra questi alcuni sono particolarmente noti sia per le loro proprietà matematiche che per l'efficacia dimostrata nelle applicazioni reali. Vogliamo mostrarne qui alcuni senza particolari esigenzea di formalizzazione teorica.
Contents
Filtro gaussiano
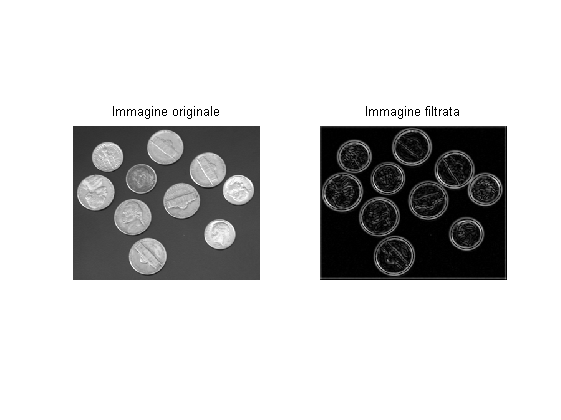
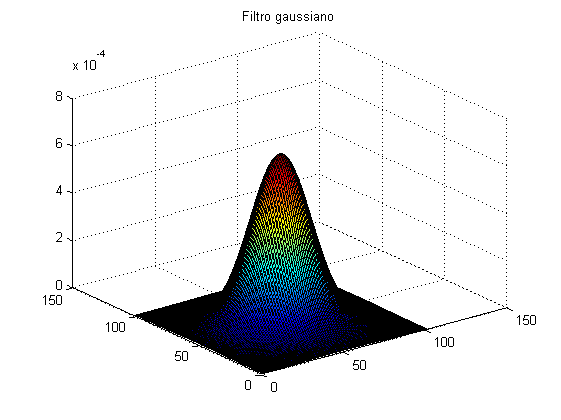
Il filtro Gaussiano consiste nel convolvere l'immagine con una risposta all'impulso consistente in una campana di Gauss centrata e normalizzata per aver somma unitaria, si tratta di un filtro separabile, quindi molto efficiente se applicato prima per righe e poi per colonne (o viceversa). Si osservi che la trasformata di Fourier di una Gaussiana è ancora una Gaussiana, quindi il filtro Gaussiano approssima un filtro passa-basso.
% Leggo l'immagine originale: img = imread('coins.png'); % Preparo la risposta all'impulso 1d: h = gauss(-50:50,15); h = h/sum(h); % Filtro le righe, le colonne, entrambe in sequenza: img1 = filter2(h,img); img2 = filter2(h',img); img3 = filter2(h',img1); % Vediamo il risultato: figure; subplot(221); imshowscale(img); title('Immagine originale'); subplot(222); imshowscale(img1); title('Filtering per righe'); subplot(223); imshowscale(img2); title('Filtering per colonne'); subplot(224); imshowscale(img3); title('Immagine filtrata');

% Vediamo l'anatomia del filtro: figure; surf(h'*h); title('Filtro gaussiano');
DoG
Se da una immagine eliminiamo le basse frequenze (ottenute con il filtro Gaussiano) rimangono le alte frequenze, ovvero i bordi:
% Vediamo la differenza di immagini filtrate con il filtro Gaussiano:
h = gauss(-5:5,1.5); h = h/sum(h);
img1 = filter2(h,img);
img3 = filter2(h',img1);
figure; imshowscale(double(img)-img3);

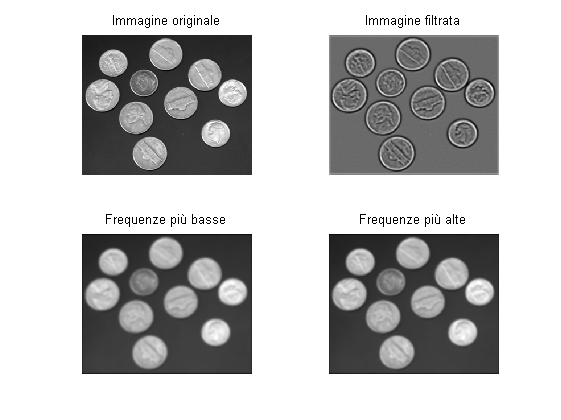
Se utilizziamo filtri Gaussiani a frequenze differenti e calcoliamo la differenza, dei risultati (o dei filtroi stessi prima di applicarli) otteniamo una specifica banda di frequenze:
% Creo due filtri a frequenze diverse: h1 = gauss(-6:6,1.8); h1 = h1/sum(h1); h2 = gauss(-6:6,1.5); h2 = h2/sum(h2); % Li applico entrambe: img1 = filter2(h1,filter2(h1',img)); img2 = filter2(h2,filter2(h2',img)); % Vediamo la composizione: figure; subplot(221); imshowscale(img); title('Immagine originale'); subplot(222); imshowscale(img2-img1); title('Immagine filtrata'); subplot(223); imshowscale(img1); title('Frequenze più basse'); subplot(224); imshowscale(img2); title('Frequenze più alte');
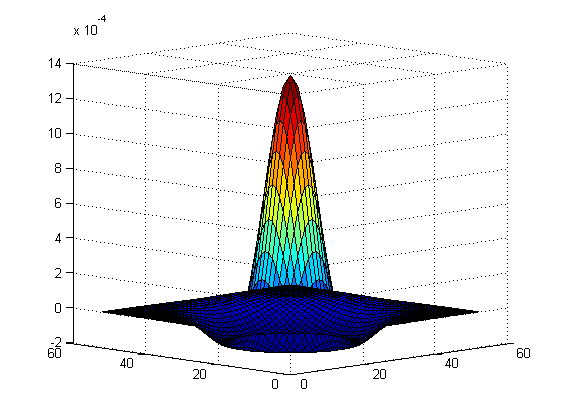
Questo filtro si chiama DoG (Difference of Gaussians) e si comporta approssimativamente come la wavelet nota con il nome di "Mexican Hat":
% Creiamone uno a frequenze più basse (per vederne meglio la forma): h1 = gauss(-26:26,7.2); h1 = h1/sum(h1); h2 = gauss(-26:26,6.0); h2 = h2/sum(h2); % Vediamolo: figure; surf(h2'*h2 - h1'*h1); view([45,45,-10]);
Derivata della Gaussiana
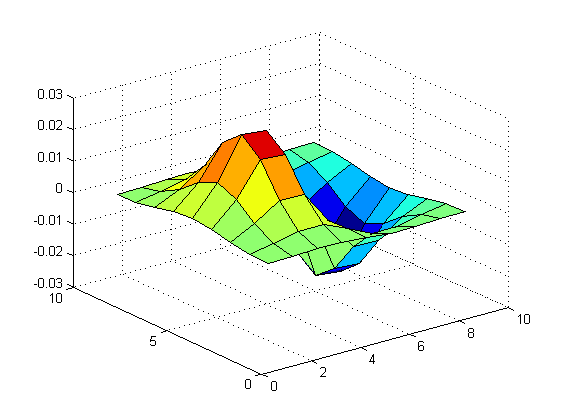
L'estrazione di bordi direzionali di angolo noto può essere ottenuta grazie ad un altro filtro ben noto: la derivata della Gaussiana. In ambito di elaborazione delle immagini la derivata 1d della Gaussiana viene utilizzata in combinazione con un filtro Gaussiano 1d ottenendo (sempre grazie alla separabilità) il seguente filtro:
% Creo i filtri 1d: g = gauss(-4:4,1.5); g = g/sum(g); dg = gaussDer(-4:4,1.5); % La derivata della gaussiana somma a zero. % Vediamolo: figure; surf(g'*dg);
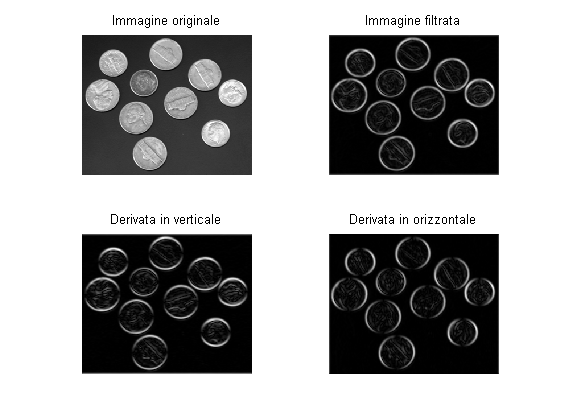
% Applico il filtro: img1 = filter2(g,filter2(dg',img)); img2 = filter2(g',filter2(dg,img)); % Vediamo i risultati: figure; subplot(221); imshowscale(img); title('Immagine originale'); subplot(222); imshowscale(abs(img1) + abs(img2)); title('Immagine filtrata'); subplot(223); imshowscale(abs(img1)); title('Derivata in verticale'); subplot(224); imshowscale(abs(img2)); title('Derivata in orizzontale');
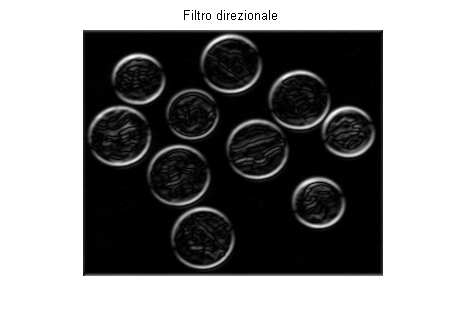
Per rendere orientabile il filtro è sufficiente comporre linearmente le immagini filtrate utilizzando i coefficienti generati da coseno e seno dell'angolo di interesse (Perché? Ragionare sulla trasformata di Fourier e sull'equazione di Eulero).
% L'angolo: alpha = 70*pi/180; % Composizione: img3 = img1*sin(alpha) + img2*cos(alpha); % Vediamo: figure; imshowscale(abs(img3)); title('Filtro direzionale');
Per convicerci "animiamo la situazione":
% Finestra in fullscreen: figure; screen_size = get(0, 'ScreenSize'); set(gcf,'Position',[0,0,screen_size(3),screen_size(4)]); % Itero sugli angoli: for alpha = 0:0.1:2*pi % Filtro: img3 = img1*sin(alpha) + img2*cos(alpha); % Mostro: clf; imshow(imscale(img3),'InitialMagnification','fit'); title('Filtro direzionale'); % Disegno e aspetto: drawnow; pause(0.1); end

Filtro Laplaciano
Nell'ambito dell'edge-detection, il filtro Laplaciano acquista la sua importanza permettendo di evidenziare bordi e zero-crossing, in particolare il Laplaciano di una funzione è definito come segue:
\Delta^2(I)=\frac{\partial^2I}{\partial x^2}+\frac{\partial^2I}{\partial y^2}ma spesso in image processing viene approssimato da un filtro convolutivo come il seguente (si osservi l'evidenziazzione delle variazioni esterne):
% Preparo i filtri: h = [0, 1, 0 1,-4, 1 0, 1, 0]; % Alternativamente: % h = [0.5, 1.0, 0.5 % 1.0,-6.0, 1.0 % 0.5, 1.0, 0.5]; % Lo applico a una scacchiera: img = checkerboard; img1 = filter2(h, img); % Vediamo: figure; subplot(121); imshow(img); title('Immagine originale'); subplot(122); imshowscale(abs(img1)); title('Immagine filtrata');

LoG
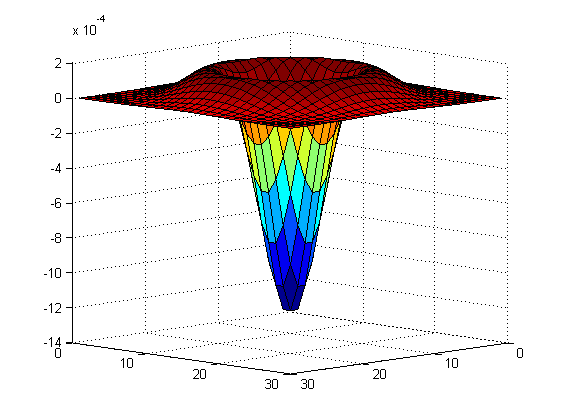
La funzione Gaussiana presenta caratteristiche interessanti anche dal punto di vista delle sue derivate parziali secode, per questo il filtro Laplacian of Gaussian (LoG) viene utilizzato per l'evidenziazione di bordi. La sua forma chiusa è:
LoG(x,y)=-\frac{1}{\pi\sigma^4}\left[1-\frac{x^2+y^2}{2\sigma^2}\right]e^{-\frac{x^2+y^2}{2\sigma^2}}% Uso la funzione di Matlab: h = fspecial('log', 30, 4); % Vediamolo: figure; surf(h); view([45,45,10]);
% Creo un LoG con frequenze accettabili: h = fspecial('log', 10, 1.5); % Applichiamo LoG all'immagine delle monete: img = imread('coins.png'); img1 = filter2(h,img); % Risultato: figure; subplot(121); imshow(img); title('Immagine originale'); subplot(122); imshowscale(abs(img1)); title('Immagine filtrata');