La compressione JPEG

La trasformata coseno, ottenuta dal caso particolare della trasformata
di Fourier per una funzione pari a valori reali, permette di passare da N
coefficienti reali nel dominio spaziale a N coefficienti reali nel
dominio della frequenza, quindi permette di mantenere l'informazione
completa nel dominio della frequenza senza modificare la quantità di
coefficienti richiesti per codificarla. A partire da questa osservazione
e considerando che la rappresentazione di una porzione di immagine nel
dominio delle frequenza porta con alta probabilità ad avere una gran
percentuale di coefficienti nulli o prossimi a zero (per tutte le
frequenza non presenti), considerando inoltre che nel caso delle immagini
quest'effetto si accentua "quadraticamente", si è deciso di utilizzare la
trasformata discreta coseno (dct) come strumento di compressione lossy
delle immagini nello standard JPEG.

Contents

Trasformata coseno di immagini

Vediamo degli esempi di trasformata coseno applicata ad una immagine di
esempio di 8x8 bit, cercando di selezionare una parte complessa di
immagine reale.

% Carico una immagine intera:
img = imtype(imread('cameraman.tif'),'gF');

% Ne prendo un pezzettino:
rect = [123,70,7,7];
img = imcrop(img,rect);

% Calcolo la trasformata coseno:
img_f = dct2(img);

% Vediamola:
imshowbig = @(img)(imshow(imresize(img,8,'nearest')));
figure;
subplot(121); imshowbig(img);
subplot(122); imshowbig(imscale(img_f));

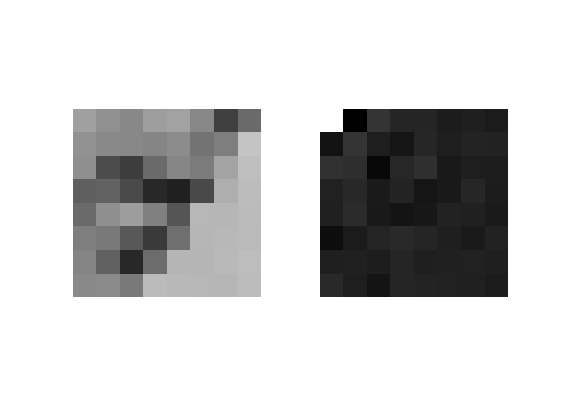
Si noti che il valor medio (coefficiente di frequenze 0,0) è l'unico a
valore elevato, il gli altri sono distribuiti attorno allo zero (con
distribuzione somigliante a una gaussiana) dove la maggior parte dei
coefficienti assume valori molto piccoli, producendo quindi variazioni
piccole nell'immagine.

% Istogramma dei coefficienti:
figure; hist(img_f(:),20);

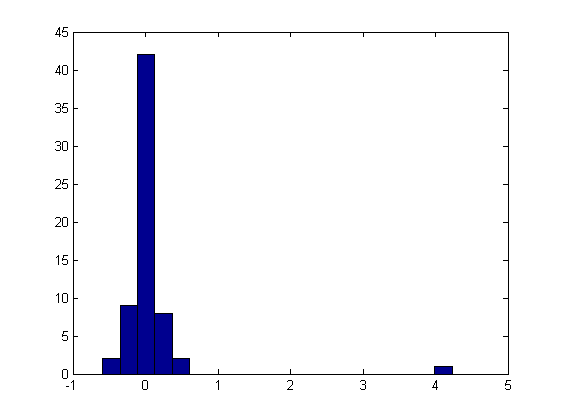
Sfruttiamo questa caratteristica per eliminare (forzando a zero) una
certa percentuale di coefficienti:

% Seleziono i coefficienti vittima:
mask = abs(img_f)<1e-1;

% Ricostruisco l'immagine:
img_f2 = img_f; img_f2(mask) = 0;
img2 =  idct2(img_f2);

% Confrontiamole:
figure;
subplot(131); imshowbig(img);
subplot(132); imshowbig(img2);
subplot(133); imshowbig(abs(img-img2));

Il risultato non è perfetto (lossy) ma ne è una buona approssimazione.
JPEG tratta blocchi 8x8, usa questa tecnica per ridurre il numero di
coefficienti, comprime tutti i coefficienti medi tramite la compressione
di Huffman (media più frequente meno bit e viceversa), codifica poi gli
altri coefficienti a "serpentina" a partire adl coefficiente medio
(escluso perché già codificato) con una tecnica simile al Run Length
Coding.

NOTA: la matrice dei coefficienti viene moltiplicata per una matrice di pesi (scelta in base al livello di compressione) condivisa dal coder e dal decoder, in questo modo vengono eliminati con più facilità i coefficienti relativi a frequenze con impatto più basso sulla percezione umana delle immagini.

Componenti della trasformata coseno

Osserviamo le componenti della trasformata coseno della nostra immagine
8x8:

% Init:
comps = zeros(64);

% Tutte le componenti:
for i=1:8
    for j=1:8
        comp = zeros(8);
        comp(i,j) = 1;
        comps((i-1)*8+1:i*8,(j-1)*8+1:j*8) = dct2(comp);
    end
end

% Vediamo:
figure; imshowscale(comps);

Un esempio fai-da-te

Proviamo a codificare una immagine, ridurre il numero di coefficienti e
ricostruire il risultato:

% Pesi di quantizzazione:
W = [ 16  11  10  16  24  40  51  61; ...
	  12  12  14  19  26  58  60  55; ...
	  14  13  16  24  40  57  69  56; ...
	  14  17  22  29  51  87  80  62; ...
	  18  22  37  56  68 109 103  77; ...
	  24  35  55  64  81 104 113  92; ...
	  49  64  78  87 103 121 120 101; ...
	  72  92  95  98 112 100 103  99 ];

% Carico l'immagine e mi preparo:
img = imtype(imread('cameraman.tif'),'gF');
img2 = zeros(size(img));
img2bis = zeros(size(img));
numZeros = 0;
numZerosBis = 0;
means = zeros(size(img,1)/8,size(img,2)/8);

% Itero sui blocchi:
for x=1:8:size(img,2)-7
    for y=1:8:size(img,1)-7
        % Ottengo il blocco:
        block = img(y:y+7,x:x+7);

        % Lo trasformo:
        block_f = dct2(block);

        % Scelgo gli zeri:
        mask = abs(255*block_f./W) < 0.25;
        maskBis = abs(255*block_f./W) < 1;
        numZeros = numZeros + sum(mask(:));
        numZerosBis = numZerosBis + sum(maskBis(:));

        % Riduco i coefficienti:
        block_f2 = block_f;
        block_f2bis = block_f;
        block_f2(mask) = 0;
        block_f2bis(maskBis) = 0;

        % Ritrasformo:
        block2 = idct2(block_f2);
        block2bis = idct2(block_f2bis);

        % Salvo:
        img2(y:y+7,x:x+7) = block2;
        img2bis(y:y+7,x:x+7) = block2bis;
        means((y-1)/8+1,(x-1)/8+1) = block_f(1);
    end
end

% Vediamole:
figure;
subplot(221); imshow(img);
title('Originale');
subplot(222); imshow(means/8); % Esercizio: scoprire perché divido per 8.
title('Le sole medie');
subplot(223); imshow(img2);
title(sprintf('%2.2f%% di zeri',100*numZeros/numel(img)));
subplot(224); imshow(img2bis);
title(sprintf('%2.2f%% di zeri',100*numZerosBis/numel(img)));

Published with MATLAB® 7.13