S_02_fourierSeries

Serie di fourier
Ortonormalità:

Serie di fourier

Fourier nell''800 intuì e dimostrò che le funzioni periodiche possono
essere scomposte come somme di funzioni trigonometriche di opportuna
frequenza e fase. In particolare se f(x+kT) = f(x) è una funzione
periodica di periodo T, allora:

f(x) = \sum_{n=-\infty}^{+\infty} c_n e^{1i n pi/T x}

dove c_k sono opportuni coefficienti che "pesano" la singola sinusoide, infatti questa serie somma infiniti termini "esponenzionale complesso" la cui frequenza della cosinusoide associata è n pi/T. Notare che se c_n = c_{-n} (coefficienti simmetrici) alloraavremmo somme di termini del tipo {e^(1i theta)+e^(-1i theta) = 2 cos(theta), caso in cui si ottiene una somma a valori reali.

I coefficienti c_n vanno scelti in maniera tale da garantire che la
serie converga alla funzione di interesse, sorvolando i dettagli
matematici (se interessano possiamo vederli assieme, la dimostrazione è
piuttosto semplice), si dimostra che:

c_n = 1/(2T) \int_{-T}^{+T} f(x) e^{-1i n pi/T x} dx

Costruiamo l'esempio con l'onda quadra, per -1<x<1:

f(x) = 0 se x<0, 1 altrimenti.

quindi integrando 1 solo dove la funzione non è nulla, e accorpando il termine n con il termine -n, otteniamo:

c_n = 1/2 \int_0^1 e^{-1i n pi x} dx
    = -\frac{1i-1i e^{-1i n pi}}{2 n pi}

Accorpando due termini della serie otteniamo:

c_n e^{1i n pi x} + c_{-n} e^{-1i n pi x} =
  = (sin(n pi x) - sin(n pi x - n pi))/(n pi)

Che (usando le regole di bisezione) vale 0 se n è pari, e vale:

2 sin(n pi x)/(n pi)

se n è dispari.

Per n=0 abbiamo 1/2 \int_0^1 e^0 dx = 1/2, quindi:

% Preparo il dominio:
X = (-2:0.01:2)';

% Calcolo:
N = 25;
a = @(n,x)(2*sin(n*pi*x)./(n*pi));
Y = cell(1,N);
comps = Y;
Y{1} = ones(size(X))/2;
comps{1} = Y{1};
for n=2:N
    comps{n} = a((n-1)*2-1,X);
    Y{n} = Y{n-1} + comps{n};
end
figure;
subplot(211); plot(X,[Y{1:5:end}]); title('Ridotte n-esime');
subplot(212); plot(X,[comps{1:5:end}]); title('Termini della serie');

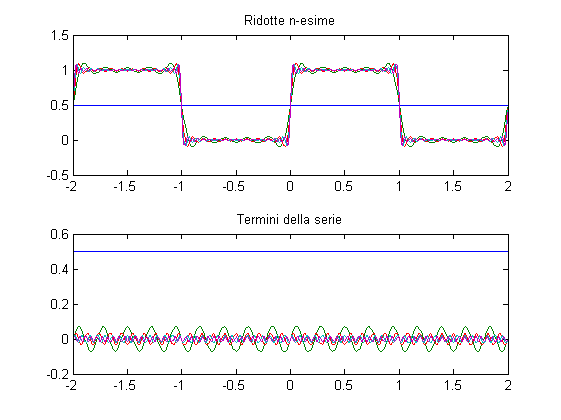
In questa scomposizione in serie le frequenze considerate sono pari alla
pulsazione omega, nella forma cos(omega x + phi), diviso 2 pi, quindi si
ha n pi /(2 pi) = n/2 (frequenze crescenti) con fase fissa pi/2.

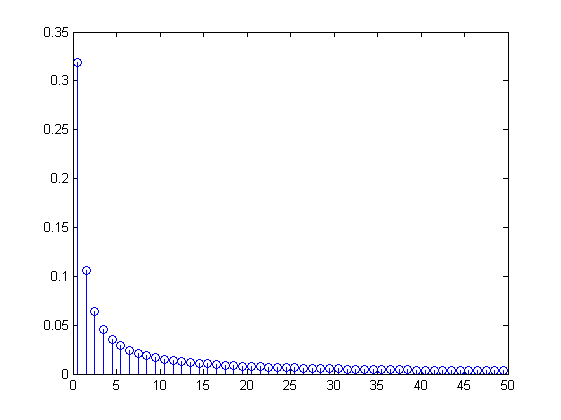
Mostriamo le ampiezze delle componenti sinusoidali ottenute, ovvero
1/(n pi) in funzione delle frequenze (notare che per 0 si ha 1/2, media
della funzione sul singolo periodo):

% Le frequenze e le ampiezze:
n = 1:2:100;
freq = n/2;
amp = 1./(n*pi);

% Vediamolo:
figure; stem(freq,amp);

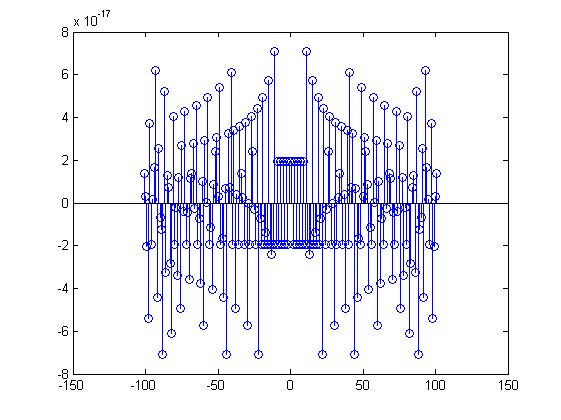
Osserviamo ora i coefficienti ottenuti per i termini della serie
completa (in cui manteniamo distinti c_n e c_{-n}.. notiamo la simmetria:

% Le frequenze e le ampiezze:
n = -101:101;
c_n = -(1i-1i*exp(-1i.*n.*pi))./(2*n*pi);

% Vediamoli:
figure; stem(n,c_n);

Ortonormalità:

La scomposizione di una funzione periodica in serie di Fourier fornisce
un numero infinito ma enumerabile di coefficienti sufficienti a
descrivere completamente la funzione stessa, inoltre la somma
esponenziali complesse di stessa frequenza produce una esponenziale
complessa di stessa frequenza e modulo differente, inoltre è possibile
moltiplicare un'esponenziale complessa per uno scalare modificando in
sostanza l'ampiezza dell'armonica... è possibile mostrare che le funzioni
periodiche sono descrivibili come punti in uno spazio vettoriale a
infinite dimensiini (spazio di Hilbert), e che la serie di Fourier
scompone tali funzioni come somma di componenti di una base dello spazio
stesso. Dimostrare l'ortonormalità della base utilizzata non è
particolarmente difficile grazie alla rappresentazione esponenziale
complessa. Dobbiamo mostrare che, dati due vettori della base
fn(x) = e^{i n pi/T x} e fm(x)e^{i m pi/T x}, il prodotto interno nello
spazio di Hilbert <fn,fm> = \int fn(x)(fm(x))* dx,
dove ()* rappresenta il coniugato complesso, assume valore 1 se n=m e 0
se n!=m:

(1/2T)\int_{-T}^T e^{i n pi/T x}(e^{i m pi/T x})* dx
  = (1/2T)\int_{-T}^T e^{i n pi/T x - i m pi/T x})* dx
  = (1/2T)\int_{-T}^T e^{i pi/T x (n - m)} dx

dove chiaramente se n==m si ha:

(1/2T)\int_{-T}^T e^0 dx = (1/2T)\int_{-T}^T e^0 = (1/2T)[x]_{-T}^T = 1

se invece n!=m allora basta dimostrare che |fn|=0:

\int_{-T}^T e^{i pi/T x n} dx
  = [e^{i pi/T x n}/(i pi/T n)]_{-T}^T
  = e^{i pi n}/(i pi/T n) - e^{-i pi n}/(i pi/T n)
  = (e^{i pi n} - e^{-i pi n})/(i pi/T n)
  = (2 sin(n pi))/(pi n)

che per n intero si annulla.

Contents

Serie di fourier

Ortonormalità: