Contact
 |
Giuliano Grossi (Associate Professor)
Dipartimento di Informatica - Università degli Studi di
Milano
Phone: +39 02503.16262 Curriculum Vitae: CV_en.pdf |
Teaching activity
- current (Italian)
-
- GPU computing (Laurea Magistrale in Informatica)
- Informazione multimediale (Laurea triennale in Informatica per la comunicazione digitale)
- Statistica e analisi dei dati (Laurea Triennale in Informatica musicale)
- past
-
- Metodi per l'elaborazione dei segnali (Laurea Magistrale in Informatica)
- Sistemi e Segnali (Laurea Triennale in Informatica)
- Programmazione in Matlab (Scuola di Fisica Medica)
- Laboratorio di programmazione Java (Laurea Triennale in Informatica)
- Elaborazione numericadei segnali (Laurea Triennale in Informatica)
- Elaborazione di segnali stocastici (Laurea Magistrale in Informatica)
Research interests
- Sparse recovery and regularization methods in signal processing
- LiMapS, k-LiMapS: We proposed a fast iterative method for finding sparse solutions to underdetermined linear systems. It is based on a fixed-point iteration scheme which combines nonconvex Lipschitzian-type mappings with canonical orthogonal projectors. The former are aimed at uniformly enhancing the sparseness level by shrinkage effects, the latter are used to project back onto the space of feasible solutions. The iterative process is driven by an increasing sequence of a scalar parameter that mainly contributes to approach the sparsest solutions. It is shown that the minima are locally asymptotically stable for a specific smooth l0-norm. Furthermore, it is shown that the points yielded by this iterative strategy are related to the optimal solutions measured in terms of a suitable smooth l1-norm. Numerical simulations on phase transition show that the performances of the proposed technique overcome those yielded by well known methods for sparse recovery.
-
In the figure we report the 3D phase transitions of LiMapS and
other sparsity solvers, such as OMP, CoSaMP, SL0, LASSO and BP. The
figure clearly shows the existence of a sharp phase transition that
partitions the phase space into a unrecoverable region, with
vanishing exact-recovery probability, from an recoverable region in
which the probability to recover the optimal sparse vector will
eventually approach to one. Qualitatively, it is evident that
LiMapS algorithm reaches the best results, having the largest area
of high recoverability.
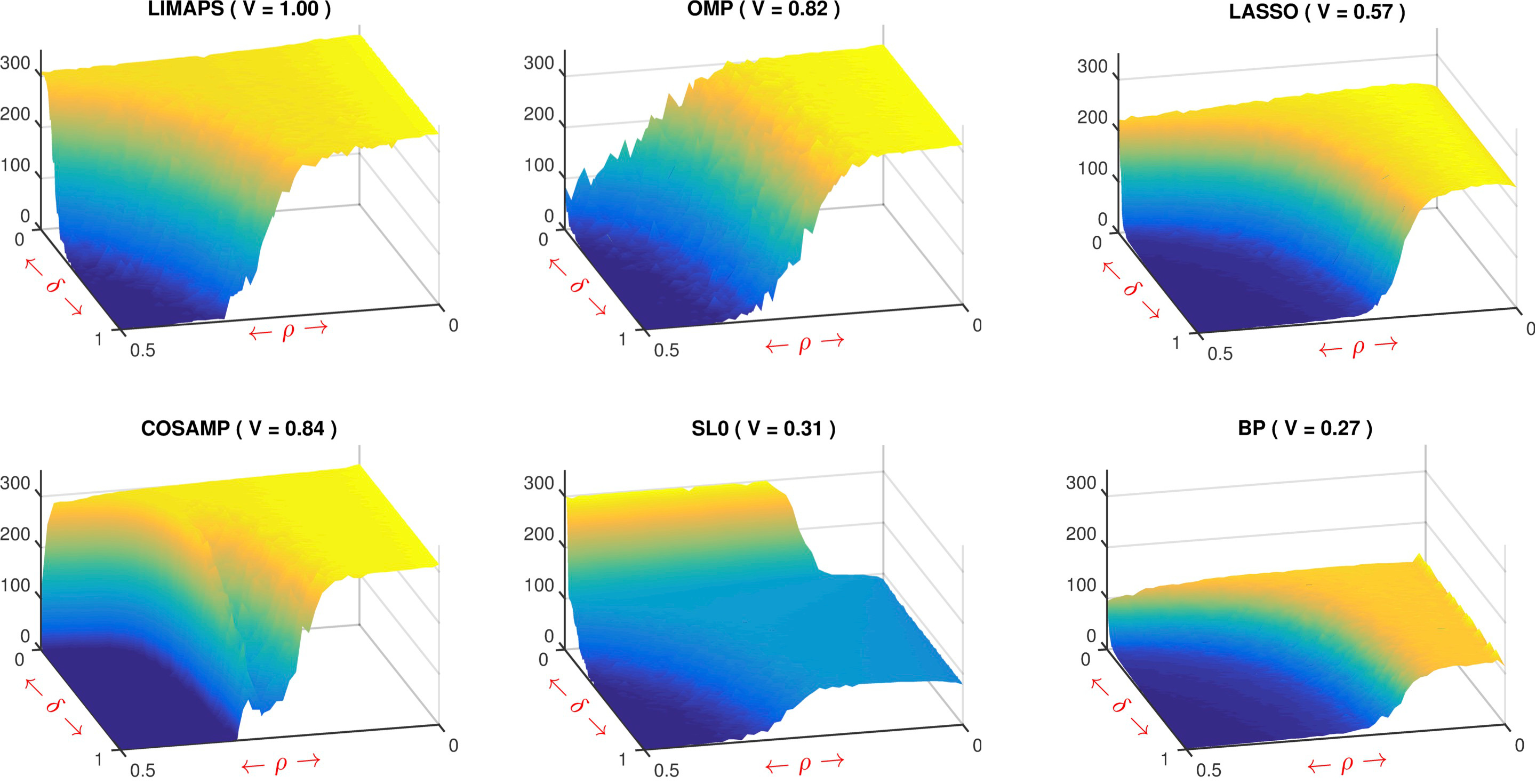
Fig. SNR of phase transitions of both l0-minimizers (first two rows) and l1-minimizers (third row) methods. The domain is defined by (δ, ρ) in [0, 1] × [0, 0.5]. Next to the method name, V represents the volume under the surface normalized to that of LiMapS. - R-SVD: In the sparse representation models, the design of overcomplete dictionaries plays a key role for the effectiveness and applicability in different domains. Recent research has produced several dictionary learning approaches, being proven that dictionaries learnt by data examples significantly outperform structured ones, e.g. wavelet transforms. In this context, learning consists in adapting the dictionary atoms to a set of training signals in order to promote a sparse representation that minimizes the reconstruction error. Finding the best fitting dictionary remains a very difficult task, leaving the question still open. A well-established heuristic method for tackling this problem is an iterative alternating scheme, adopted for instance in the well-known K-SVD algorithm. Essentially, it consists in repeating two stages; the former promotes sparse coding of the training set and the latter adapts the dictionary to reduce the error. In this context we presented R-SVD, a new method that, while maintaining the alternating scheme, adopts the Orthogonal Procrustes analysis to update the dictionary atoms suitably arranged into groups. Comparative experiments on synthetic data prove the effectiveness of R-SVD with respect to well known dictionary learning algorithms such as K-SVD, ILS-DLA and the online method OSDL. Moreover, experiments on natural data such as ECG compression, EEG sparse representation, and image modeling confirm the R-SVD robustness and wide applicability.
-
ECG compression: Long duration recordings of ECG
signals require high compression ratios, in particular when storing
on portable devices. Most of the ECG compression methods in
literature are based on wavelet transform while only few of them
rely on sparsity promotion models. We proposed a novel ECG signal
compression framework based on sparse representation using a set of
ECG segments as natural basis. This approach exploits the signal
regularity, i.e. the repetition of common patterns, in order to
achieve high compression ratio (CR). We applied k-LiMapS as fine-
tuned sparsity solver algorithm guaranteeing the required signal
reconstruction quality (PRD). The idea behind the method relies on
basis elements drawn from the initial transitory of a signal
itself, and the sparsity promotion process applied to its
subsequent blocks grabbed by a sliding window. The saved
coefficients rescaled in a convenient range, quantized and
compressed by a lossless entropy-based algorithm. Extensive
experiments of our method and of four competitors (namely ARLE,
Rajoub, SPIHT, TRE) have been conducted on all the 48 records of
MIT-BIH Arrhythmia Database. Our method achieves average
performances that are 3 times higher than the competitor results.
In particular the compression ratio gap between our method and the
others increases with the PRD growing.
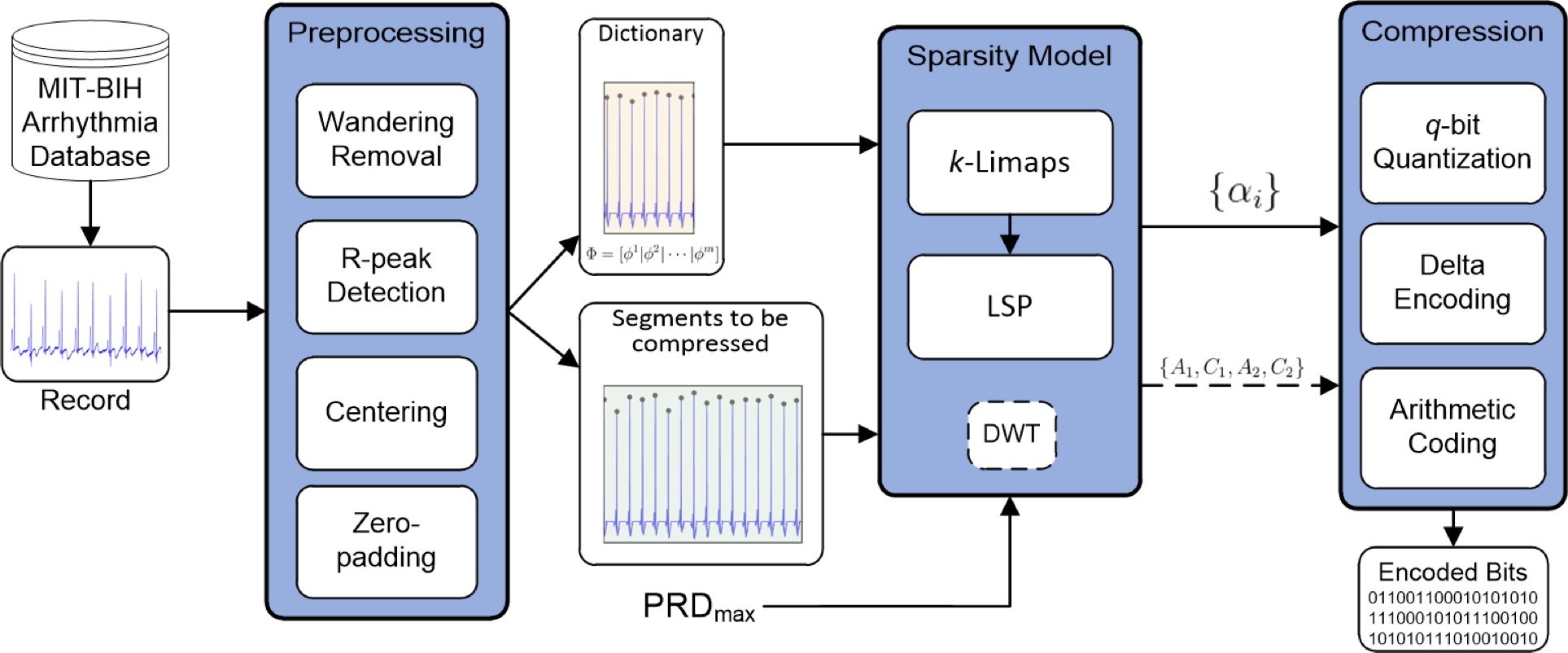
Fig. Block diagram of the ECG signal compression process, showing the principal elements of our framework. Stage 1. Signal preprocessing through standard filtering for wandering removal, R-peaks detection and normalization based on zero-padding of centered RR-segments. Stage 2. Dictionary construction over natural basis extracted from the initial transient of the normalized record. Stage 3. Online sparse decomposition via the sparsity solver k-LiMapS combined to the least-squares projection (LSP) and resorting to the DWT in case of either long or non-sparsifiable segments. Stage 4. Quantization and compression of the coefficients carried out both by the sparsity processand (possibly) by DWT using the arithmetic coding. - Face recognition via sparse decomposition
-
SSPP problem: Single Sample Per Person (SSPP) Face
Recognition is receiving a significant attention due to the
challenges it opens especially when conceived for real applications
under unconstrained environments. We proposed a solution combining
the effectiveness of deep convolutional neural networks (DCNN)
feature characterization, the discriminative capability of linear
discriminant analysis (LDA), and the efficacy of a sparsity based
classifier built on the k-LiMapS algorithm. Experiments on the
public LFW dataset prove the method robustness to solve the SSPP
problem, outperforming several state-of-the-art methods.
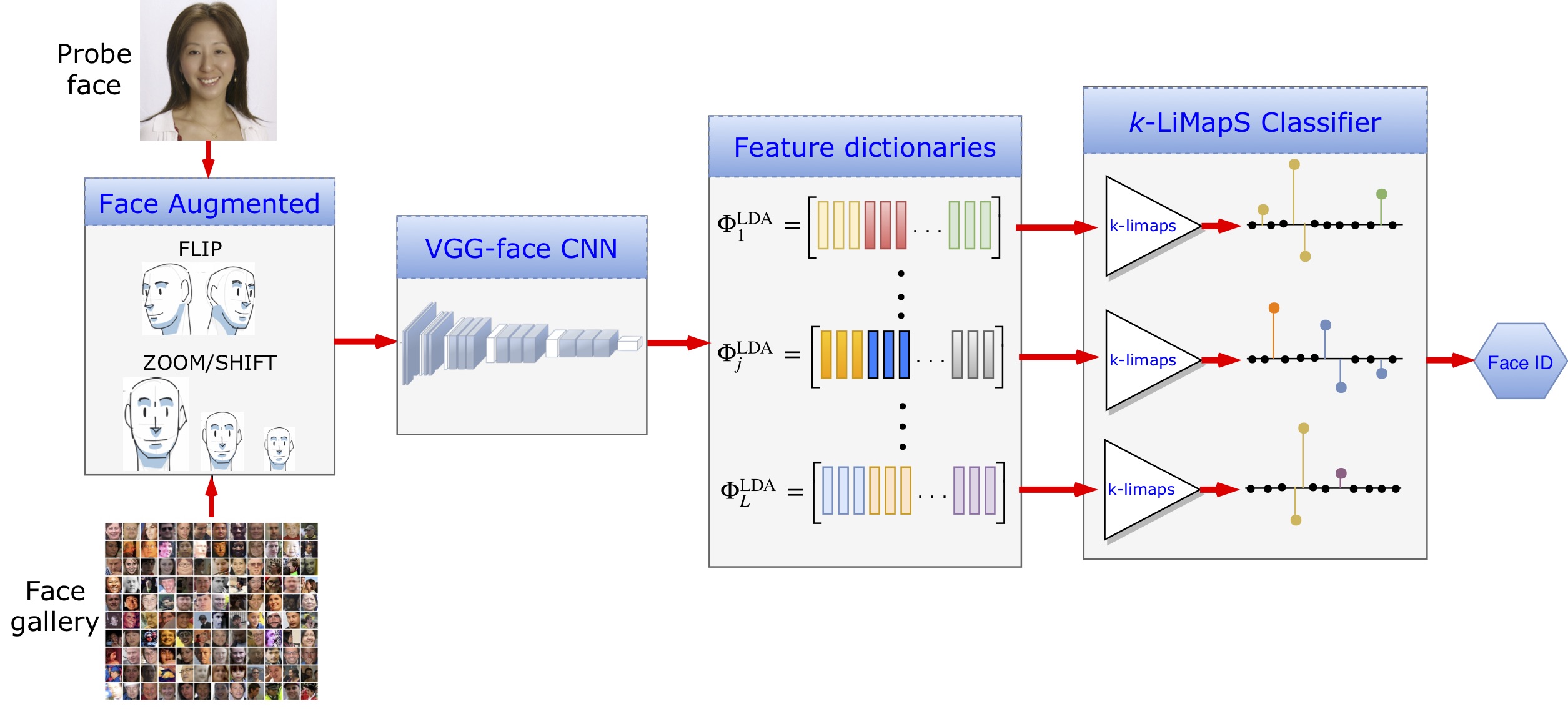
Fig. Block diagram (below in the figure) of the classification process. First, image augmentation, second, feature characterization via DCNN, third, data organization in dictionaries and LDA transformation, finally k-LiMapS classifier to produce the face identity. -
FR framework (very few images per subject): For
decades, face recognition (FR) has attracted a lot of attention,
and several systems have been successfully developed to solve this
problem. However, the issue deserves further research e®ort so as
to reduce the still existing gap between the computer and human
ability in solving it. Among the others, one of the human skills
concerns his ability in naturally conferring a degree of
reliability" to the face identi ̄cation he carried out. We believe
that providing a FR system with this feature would be of great help
in real application contexts, making more °exible and treatable the
identi ̄cation process. In this spirit, we propose a completely
automatic FR system robust to possible adverse illuminations and
facial expression variations that provides together with the
identity the corresponding degree of reliability. The method
promotes sparse coding of multi-feature representations with LDA
projections for dimensionality reduction, and uses a multistage
classi ̄er. The method has been evaluated in the challenging
condition of having few (3–5) images per subject in the gallery.
Extended experiments on several challenging databases (frontal
faces of Extended YaleB, BANCA, FRGC v2.0, and frontal faces of
Multi-PIE) show that our method outperforms several
state-of-the-art sparse coding FR systems, thus demon- strating its
e®ectiveness and generalizability.
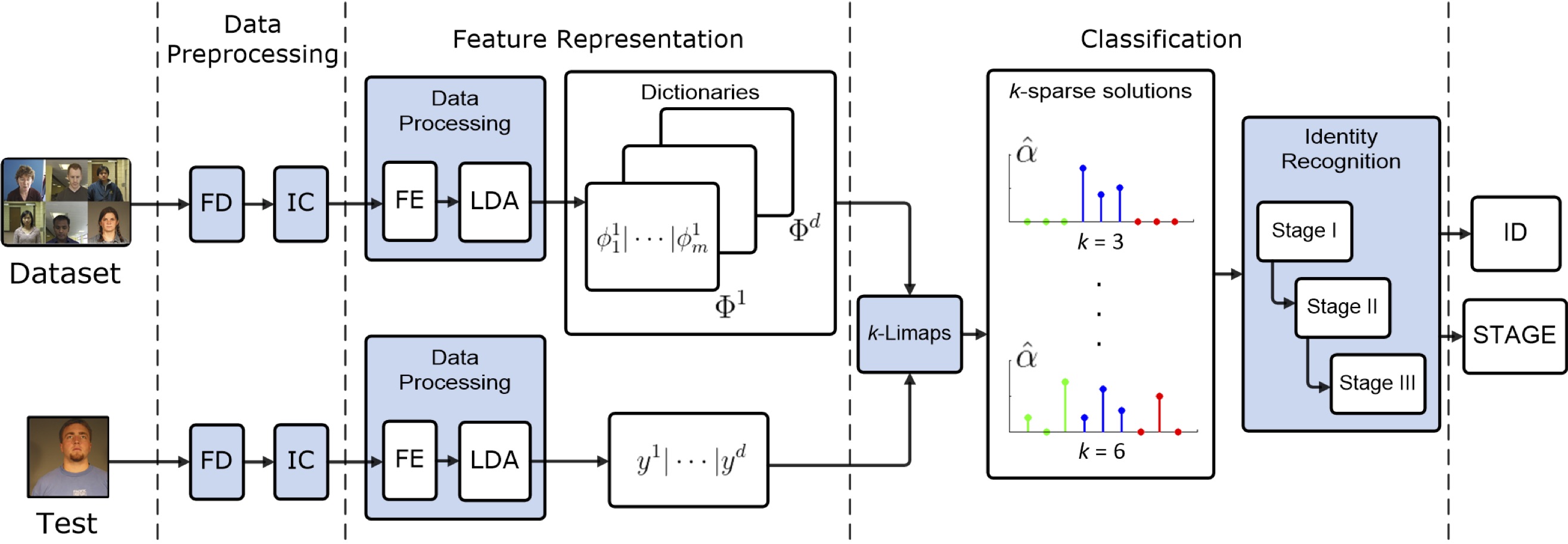
Fig. The proposed method consists of three modules. 1.Data Preprocessing: based on the Face Detection (FD) and the Illumination Corrections (IC). 2.Feature Representation: built on Feature Extraction (FE), projection in the LDA space, and the dictionary and test vector construction. 3.Classification: uses the k-LiMapS SR method and the multi-stage Identity Recognition module; examples of ideal sparse solutions for k = 3, 6 are depicted, where the blue positions, corresponding to the right subject, are very present in the support. - Stochastic models in affective computing
-
Deep models for the affective space We draw on a
simulationist approach to the analysis of facially displayed
emotions - e.g., in the course of a face-to-face interaction
between an expresser and an observer. At the heart of such
perspective lies the enactment of the perceived emotion in the
observer. We propose a novel probabilistic framework based on a
deep latent representation of a continuous affect space, which can
be exploited for both the estimation and the enactment of affective
states in a multimodal space (visible facial expressions and
physiological signals). The rationale behind the approach lies in
the large body of evidence from affective neuroscience showing that
when we observe emotional facial expressions, we react with
congruent facial mimicry. Further, in more complex situations,
affect understanding is likely to rely on a comprehensive
representation grounding the reconstruction of the state of the
body associated with the displayed emotion. We show that our
approach can address such problems in a unified and principled
perspective, thus avoiding ad hoc heuristics while minimising
learning efforts. Results so far achieved have been assessed by
exploiting a publicly available dataset.
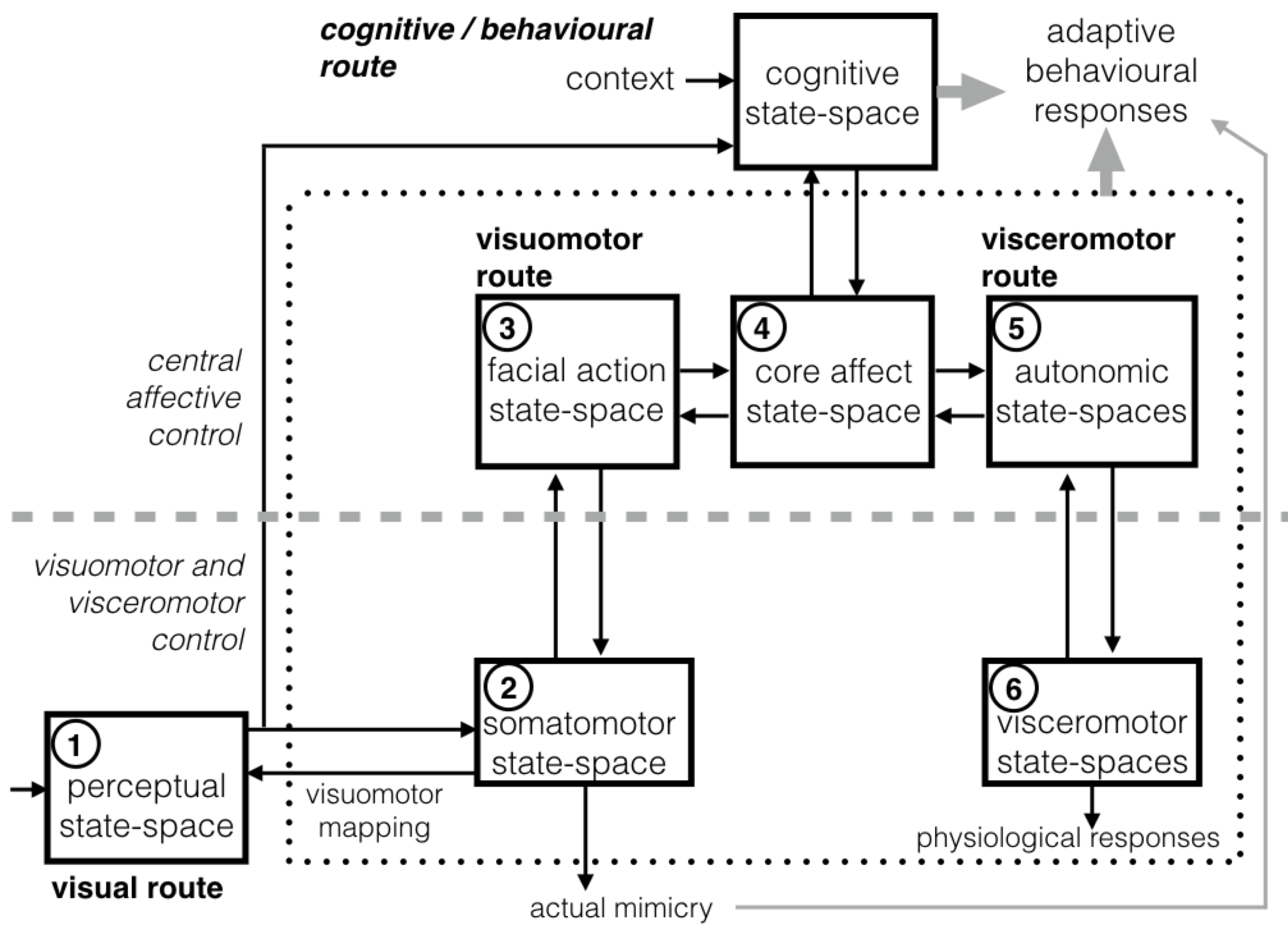
Fig. The functional architecture for face-based emotion understanding. It provides an high-level decomposition of the neural architecture outlined in Fig. 1 into major components together with a characterisation of the interaction of the components. Numbered components are those considered in this study and numbering follows their presentation in text. To keep to the neural architecture, and 1 -> 2 -> 3 -> 4 and 6 -> 5 -> 4 one-head arrows indicate “forward”, bottom-up projections; 1 <- 2 <- 3 <- 4 and 6 <- 5 <- 4 denote “backward”, top-down projections. The visual system for dynamic facial expression perception interacts with an extended system, which involves the emotion system (dotted box) and high level cognitive/conceptual processes. Interaction is regulated by the visuomotor mediation of a component for action perception. The latter transforms the sensory information of observed facial actions into the observer’s own somatomotor representations. The activation of the visuomotor route in turn triggers visceromotor reactions through the mediation of the core affect state-space. From there the loop of simulation- based dynamics involving all components unfolds to support the whole process. Dashed grey lines distinguish between the hierarchical levels of control. - Parallel algorithms on GPU-based architectures
-
ParCOSNET: Several problems in network biology and
medicine can be cast into a framework where entities are
represented through partially labeled networks, and the aim is
inferring the labels usually binary of the unlabeled part.
Connections represent functional or genetic similarity between
entities, while the labellings often are highly unbalanced, that is
one class is largely under-represented: for instance in the
automated protein function prediction (AFP) for most Gene Ontology
terms only few proteins are annotated, or in the disease-gene
prioritization problem only few genes are actually known to be
involved in the etiology of a given disease. Imbalance-aware
approaches to accurately predict node labels in biological networks
are thereby required. Furthermore, such methods must be scalable,
since input data can be large-sized as, for instance, in the
context of multi-species protein networks.
We proposed a novel semi-supervised parallel enhancement of COSNET, an imbalance-aware algorithm build on Hopfield neural model recently suggested to solve the AFP problem. By adopting an efficient representation of the graph and assuming a sparse network topology, we empirically show that it can be efficiently applied to networks with millions of nodes. The key strategy to speed up the computations is to partition nodes into independent sets so as to process each set in parallel by exploiting the power of GPU accelerators. This parallel technique ensures the convergence to asymptotically stable attractors, while preserving the asynchronous dynamics of the original model. Detailed experiments on real data and artificial big instances of the problem highlight scalability and efficiency of the proposed method.
By parallelizing COSNET we achieved on average a speed-up of 180x in solving the AFP problem in the S. cerevisiae, Mus musculus and Homo sapiens organisms, while lowering memory requirements. In addition, to show the potential applicability of the method to huge biomolecular networks, we predicted node labels in artificially generated sparse networks involving hundreds of thousands to millions of nodes.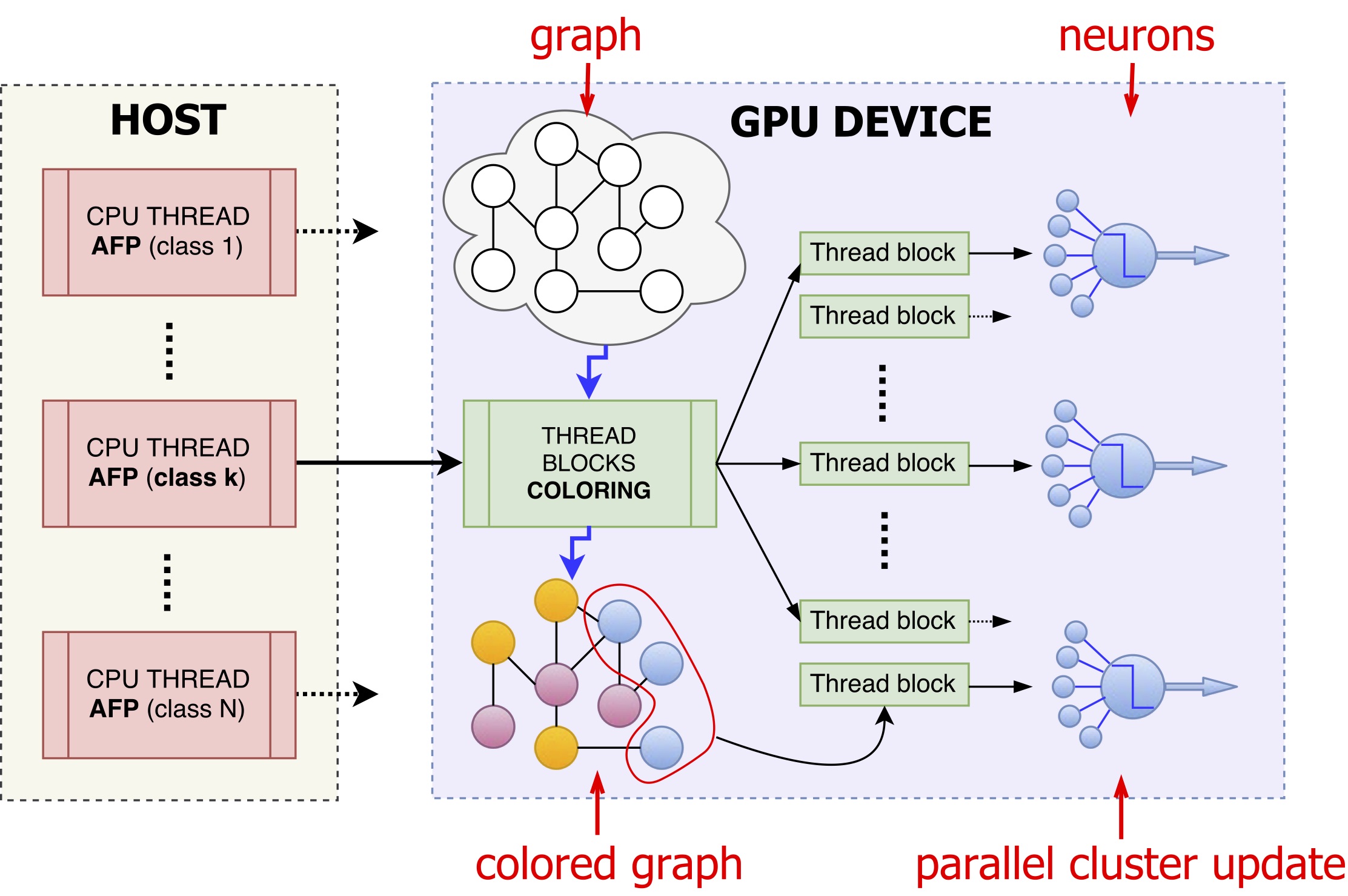
Fig. CPU/GPU schema of the ParCOSNET parallelization. Multiple CPU threads are launched in parallel each one solving the AFP problem for a given class/protein function. The GPU thread blocks, each composed of several CUDA threads, first solve the coloring problem for the graph and then concurrently process all neurons of a given color, for all colors in sequence. A further fine-grained level of parallelism is finally introduced by assigning to each neuron a thread block to perform the neuron level local computations. -
Accelerated VP8 ME: We developed an efficient
cooperative interaction between multicore (CPU) and manycore (GPU)
resources in the design of a high-performance video encoder. The
proposed technique, applied to the well-establi\-shed and highly
optimized VP8 encoding format, can achieve a significant speed-up
with respect to the mostly optimized software encoder (up to
$\times$6), with minimum degradation of the visual quality and low
processing latency. This result has been obtained through a highly
optimized CPU-GPU interaction, the exploitation of specific GPU
features, and a modified search algorithm specifically adapted to
the GPU execution model. Several experimental results are reported
and discussed, confirming the effectiveness of the proposed
technique. The presented approach, though implemented for the VP8
standard, is of general interest, as it could be applied to any
other video encoding scheme.

Fig. Block diagram of the VP8 encoding scheme. Motion Estimation plays a major role in the inter-frame prediction and it is one of the most computationally-intensive tasks of the whole encoding process. - Heart rate estimation by video techniques
-
pyVHR framework: (short for Python framework for Virtual Heart Rate) is a comprehensive framework for
studying methods of pulse rate
estimation relying on remote photoplethysmography (rPPG). The methodological rationale behind the framework is that in
order to study, develop and compare new rPPG methods in a principled and reproducible way, the following conditions
should be met: i) a structured pipeline to monitor rPPG algorithms' input, output, and main control parameters; ii)
the
availability and the use of multiple datasets; iii) a sound statistical assessment of methods' performance. pyVHR
allows
to easily handle rPPGmethods and data, while simplifying the statistical assessment.
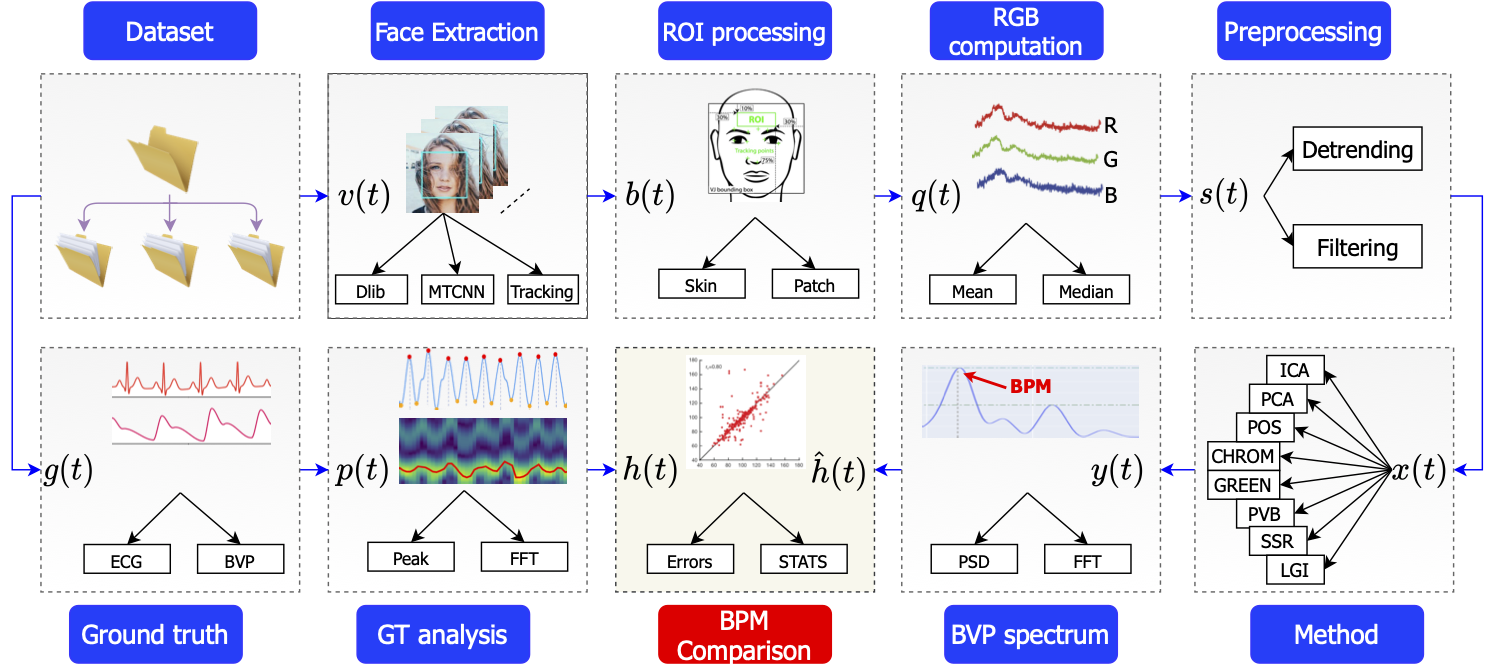
Fig. Overall pyVHR framework schema.
Projects
- [2019-2021]
- National project Fondazione Cariplo (N. 2018-0858). Project title: “Stairway to elders: bridging space, time and emotions in their social environment for wellbeing”, progetto sul bando "Ricerca Sociale sull’invecchiamento: persone, luoghi e relazioni" (Fondazione Cariplo nell’anno 2018).
- [2013-2016]
- European project FP7-ICT-2013-11: Future Networks. Project title: Network Functions as-a-Service over Virtualised Infrastructures (T-NOVA), project number 619520.
- [2013-2016]
- National project Futuro in Ricerca (FIRB) program. Project title: Interpreting emotions: a computational tool integrating facial expressions and biosignals based shape analysis and bayesian networks, Founded by MIUR - Ministero dell'Istruzione dell'Università e della Ricerca.
- [2001-2002]
- National research project COFIN. Project title: Modelli di calcolo innovativi: metodi sintattici e combinatori, Founded by MIUR - Ministero dell'Istruzione dell'Università e della Ricerca.
- [1998-2001]
- National project with title Progetto Finalizzato Biotecnologie. Work: Studio e sviluppo di un sistema software per il controllo in tempo reale di esperimenti di misura del calcio intracellulare (Atti del Convegno del Progetto Finalizzato Biotecnologie Genova 2000).
PhD student
- [2021]
- Alessandro D'Amelio (A stochastic foraging model of attentive eye guidance on dynamic stimuli, supervisor)
- [2021]
- Alessandro Petrini (High Performance Computing Machine Learning Methods For Precision Medicine, co-supervisor)
- [2013]
- Alessandro Adamo (Sparse recovery by nonconvex Lipshitzian mappings, co-supervisor)
- [2006]
- Massimo Marchi (Back and forth between Grid/Web Services and declarative specification, co-supervisor)
Software
- pyVHR framework
-
A comprehensive framework for studying methods of pulse rate estimation
relying on remote photoplethysmography (rPPG).
- pyVHR on github
- The LiMapS algorithm
-
A new regularization method for sparse recovery based on a
fixed-point iteration schema which combines Lipschitzian-type
mappings and orthogonal projectors
- LiMaps package for MATLAB
- The k-LiMapS algorithm
-
A new algorithm to solve the sparse approximation problem over
redundant dictionaries based on LiMapS, but retaining the best k
basis (or dictionary) atoms
- k-LiMaps package for MATLAB
- The PrunICA algorithm
-
PrunICA is way to speed-up the FastICA-like algorithms by a
controlled random pruning of the input mixtures, both on the entire
mixture or on fixed-size blocks when segmented
- PrunICA package for MATLAB
Papers
-
- M. Rahman, M. Jannat, M. Islam, G. Grossi, S. Bursic, M. Aktaruzzaman
- Real-time face mask position recognition system based on MobileNet model
- Smart Health 28, pp. 100382, 2023
-
- G. Boccignone, A. D’Amelio, O. Ghezzi, G. Grossi, R. Lanzarotti
- An Evaluation of Non-Contact Photoplethysmography-Based Methods for Remote Respiratory Rate Estimation
- Sensors 23(7), pp. 3387, 2023
-
- G. Boccignone, S. Bursic, V. Cuculo, A. D’Amelio, G. Grossi, R. Lanzarotti, S. Patania
- DeepFakes Have No Heart: A Simple rPPG-Based Method to Reveal Fake Videos
- Image Analysis and Processing--ICIAP 2022: 21st International Conference, Lecce, Italy, May 23--27, 2022, Proceedings, Part II, pp. 186-195, 2022
-
- D. Conte, J. Ramel, G. Grossi, R. Lanzarotti, J. Lin
- Editorial message Special Track on Graph Models for Learning and Recognition
- SAC22: Proceedings of the 37th ACM/SIGAPP Symposium on Applied Computing, pp. 568-568, 2022
-
- G. Boccignone, D. Conte, V. Cuculo, A. D’Amelio, G. Grossi, R. Lanzarotti, E. Mortara
- pyVHR: a Python framework for remote photoplethysmography
- PeerJ Computer Science 8, pp. e929, 2022 [doi]
-
- F. Odone, G. Grossi, R. Lanzarotti, H. Medeiros, N. Noceti
- Guest Editorial Assistive Computing Technologies for Human Well-Being
- IEEE Transactions on Emerging Topics in Computing 9(3), pp. 1231-1233, 2021 [doi]
-
- D. Conte, G. Grossi, R. Lanzarotti, J. Lin, A. Petrini
- Analysis of a parallel MCMC algorithm for graph coloring with nearly uniform balancing
- Pattern Recognition Letters 149, pp. 30-36, 2021
-
- S. Bursic, A. D'Amelio, M. Granato, G. Grossi, R. Lanzarotti
- A Quantitative Evaluation Framework of Video De-Identification Methods
- 2020 25th International Conference on Pattern Recognition (ICPR), pp. 6089-6095, 2021 [doi]
-
- C. Ba, E. Casiraghi, M. Frasca, J. Gliozzo, G. Grossi, M. Mesiti, M. Notaro, P. Perlasca, A. Petrini, M. Re
- A Graphical Tool for the Exploration and Visual Analysis of Biomolecular Networks
- Computational Intelligence Methods for Bioinformatics and Biostatistics: 15th International Meeting, CIBB 2018, Caparica, Portugal, September 6--8, 2018, Revised Selected Papers, pp. 88-98, 2020
-
- M. Frasca, M. Sepehri, A. Petrini, G. Grossi, G. Valentini
- Committee-Based Active Learning to Select Negative Examples for Predicting Protein Functions
- Computational Intelligence Methods for Bioinformatics and Biostatistics, pp. 80-87, 2020
-
- M. Frasca, G. Grossi, G. Valentini
- Multitask Hopfield Networks
- Machine Learning and Knowledge Discovery in Databases, pp. 349-365, 2020
-
- G. Boccignone, C. de'Sperati, M. Granato, G. Grossi, R. Lanzarotti, N. Noceti, F. Odone
- Stairway to Elders: Bridging Space, Time and Emotions in Their Social Environment for Wellbeing
- ICPRAM, pp. 548-554, 2020
-
- A. Petrini, M. Mesiti, M. Schubach, M. Frasca, D. Danis, M. Re, G. Grossi, L. Cappelletti, T. Castrignanò, P. Robinson, G. Valentini
- parSMURF, a high-performance computing tool for the genome-wide detection of pathogenic variants
- GigaScience 9(5), pp. giaa052, 2020 [doi]
-
- G. Grossi, R. Lanzarotti, P. Napoletano, N. Noceti, F. Odone
- Positive technology for elderly well-being: A review
- Pattern Recognition Letters 137, pp. 61-70, 2020 [doi]
-
- G. Grossi, P. Paglierani, F. Pedersini, A. Petrini
- Enhanced multicore--manycore interaction in high-performance video encoding
- Journal of Real-Time Image Processing 17(4), pp. 887-902, 2020
-
- G. Boccignone, D. Conte, V. Cuculo, A. D’Amelio, G. Grossi, R. Lanzarotti
- An Open Framework for Remote-PPG Methods and their Assessment
- IEEE Access 8, pp. 216083-216103, 2020 [doi]
-
- G. Boccignone, V. Cuculo, A. D’Amelio, G. Grossi, R. Lanzarotti
- On Gaze Deployment to Audio-Visual Cues of Social Interactions
- IEEE Access 8, pp. 161630-161654, 2020 [doi]
-
- J. Gliozzo, P. Perlasca, M. Mesiti, E. Casiraghi, V. Vallacchi, E. Vergani, M. Frasca, G. Grossi, A. Petrini, M. Re, A. Paccanaro, G. Valentini
- Network modeling of patients' biomolecular profiles for clinical phenotype/outcome prediction
- Scientific reports 10(1), pp. 1-15, 2020 [doi]
-
- G. Boccignone, V. Cuculo, A. D'Amelio, G. Grossi, R. Lanzarotti
- Give Ear to My Face: Modelling Multimodal Attention to Social Interactions
- Computer Vision -- ECCV 2018 Workshops, pp. 331-345, 2019
-
- V. Cuculo, A. D'Amelio, G. Grossi, R. Lanzarotti
- Worldly Eyes on Video: Learnt vs. Reactive Deployment of Attention to Dynamic Stimuli
- Image Analysis and Processing -- ICIAP 2019, pp. 128-138, 2019
-
- D. Conte, G. Grossi, R. Lanzarotti, J. Lin, A. Petrini
- A Parallel MCMC Algorithm for the Balanced Graph Coloring Problem
- Graph-Based Representations in Pattern Recognition, pp. 161-171, 2019
-
- P. Perlasca, M. Frasca, C. Ba, M. Notaro, A. Petrini, E. Casiraghi, G. Grossi, J. Gliozzo, G. Valentini, M. Mesiti
- UNIPred-Web: a web tool for the integration and visualization of biomolecular networks for protein function prediction
- BMC Bioinformatics 20(1), pp. 422, 2019
-
- N. Zhou, e. al.
- The CAFA challenge reports improved protein function prediction and new functional annotations for hundreds of genes through experimental screens
- Genome Biology 20(1), pp. 244, 2019
-
- V. Cuculo, A. D'amelio, G. Grossi, R. Lanzarotti, J. Lin
- Robust Single Sample Face Recognition by Sparse Recovery on Learnt Dictionary of Deep-CNN Features
- Sensors 19(1), 2019 [doi]
-
- M. Frasca, G. Grossi, J. Gliozzo, M. Mesiti, M. Notaro, P. Perlasca, A. Petrini, G. Valentini
- A GPU-based algorithm for fast node label learning in large and unbalanced biomolecular networks
- BMC Bioinformatics 19(10), pp. 353, 2018 [doi]
-
- G. Boccignone, D. Conte, V. Cuculo, A. D'Amelio, G. Grossi, R. Lanzarotti
- Deep Construction of an Affective Latent Space via Multimodal Enactment
- IEEE Transactions on Cognitive and Developmental Systems 10(4), pp. 865-880, 2018 [doi]
-
- G. {Boccignone}, M. {Bodini}, V. {Cuculo}, G. {Grossi}
- Predictive Sampling of Facial Expression Dynamics Driven by a Latent Action Space
- 2018 14th International Conference on Signal-Image Technology Internet-Based Systems (SITIS), pp. 143-150, 2018 [doi]
-
- M. Bodini, A. D'Amelio, G. Grossi, R. Lanzarotti, J. Lin
- Single Sample Face Recognition by Sparse Recovery of Deep-Learned LDA Features
- Advanced Concepts for Intelligent Vision Systems, pp. 297-308, 2018 [doi]
-
- D. Cusumano, M. Fumagalli, F. Ghielmetti, L. Rossi, G. Grossi, R. Lanzarotti, L. Fariselli, E. De
- Sum signal dosimetry: A new approach for high dose quality assurance with Gafchromic EBT3
- Journal of Applied Clinical Medical Physics, 2017 [doi]
-
- A. Adamo, G. Grossi, R. Lanzarotti, J. Lin
- Sparse decomposition by iterating Lipschitzian-type mappings
- Theoretical Computer Science 664, pp. 12 - 28, 2017 [doi]
-
- G. Grossi, R. Lanzarotti, J. Lin
- Orthogonal Procrustes Analysis for Dictionary Learning in Sparse Linear Representation
- PLOS ONE 12(1), pp. 1-16, 2017 [doi]
-
- C. Ceruti, V. Cuculo, A. D'Amelio, G. Grossi, R. Lanzarotti
- Taking the Hidden Route: Deep Mapping of Affect via 3D Neural Networks
- New Trends in Image Analysis and Processing (ICIAP 2017), pp. 189-196, 2017 [doi]
-
- G. Boccignone, V. Cuculo, G. Grossi, R. Lanzarotti, R. Migliaccio
- Virtual EMG via Facial Video Analysis
- Image Analysis and Processing (ICIAP 2017), pp. 197-207, 2017 [doi]
-
- A. D'Amelio, V. Cuculo, G. Grossi, R. Lanzarotti, J. Lin
- A Note on Modelling a Somatic Motor Space for Affective Facial Expressions
- New Trends in Image Analysis and Processing (ICIAP 2017), pp. 181-188, 2017 [doi]
-
- D. Cusumano, M. Fumagalli, F. Ghielmetti, L. Rossi, G. Grossi, R. Lanzarotti, L. Fariselli, E. {De Martin}
- A.53 - Sum signal film dosimetry: A novel approach for high dose patient specific quality assurance with Gafchromic EBT3
- Physica Medica 32, pp. 16, 2016 [doi]
-
- P. Paglierani, G. Grossi, F. Pedersini, A. Petrini
- GPU-based VP8 encoding: Performance in native and virtualized environments
- 2016 International Conference on Telecommunications and Multimedia (TEMU 2016), pp. 1-5, 2016 [doi]
-
- P. Comi, P. Crosta, M. Beccari, P. Paglierani, G. Grossi, F. Pedersini, A. Petrini
- Hardware-accelerated high-resolution video coding in Virtual Network Functions
- 2016 European Conference on Networks and Communications (EuCNC 2016), pp. 32-36, 2016 [doi]
-
- G. Grossi, R. Lanzarotti, J. Lin
- Robust Face Recognition Providing the Identity and Its Reliability Degree Combining Sparse Representation and Multiple Features
- International Journal of Pattern Recognition and Artificial Intelligence 30(10), pp. 1656007, 2016 [doi]
-
- G. Grossi, R. Lanzarotti, J. Lin
- A Selection Module for Large-Scale Face Recognition Systems
- Image Analysis and Processing (ICIAP 2015) - 18th International Conference, pp. 529-539, 2015 [doi]
-
- D. Cusumano, M. Fumagalli, F. Ghielmetti, L. Rossi, G. Grossi, R. Lanzarotti, L. Fariselli, E. De
- OC-0556: Sum signal dosimetry: a novel approach for high dose patient specific quality assurance with Gafchromic EBT3
- Radiotherapy and Oncology 115, pp. S270-S271, 2015
-
- A. Adamo, G. Grossi, R. Lanzarotti, J. Lin
- Robust face recognition using sparse representation in LDA space
- Machine Vision and Applications 26(6), pp. 837-847, 2015 [doi]
-
- A. Adamo, G. Grossi, R. Lanzarotti, J. Lin
- ECG compression retaining the best natural basis k-coefficients via sparse decomposition
- Biomed. Signal Proc. and Control 15, pp. 11-17, 2015 [doi]
-
- G. Grossi, R. Lanzarotti, J. Lin
- High-rate compression of ECG signals by an accuracy-driven sparsity model relying on natural basis
- Digital Signal Processing 45, pp. 96-106, 2015 [doi]
-
- A. Adamo, G. Grossi, R. Lanzarotti
- Face Recognition in Uncontrolled Conditions Using Sparse Representation and Local Features
- Image Analysis and Processing (ICIAP 2013) - 17th International Conference, pp. 31-40, 2013 [doi]
-
- A. Adamo, G. Grossi, R. Lanzarotti
- Local features and sparse representation for face recognition with partial occlusions
- IEEE International Conference on Image Processing (ICIP 2013), pp. 3008-3012, 2013 [doi]
-
- A. Adamo, G. Grossi, R. Lanzarotti
- Sparse Representation Based Classification for Face Recognition by k-LiMapS Algorithm
- Image and Signal Processing - 5th International Conference (ICISP 2012), pp. 245-252, 2012 [doi]
-
- A. Adamo, G. Grossi
- A fixed-point iterative schema for error minimization in k-sparse decomposition
- IEEE Int. Symp. on Signal Processing and Information Technology (ISSPIT 2011), pp. 167-172, 2011 [doi]
-
- A. Adamo, G. Grossi
- Sparsity recovery by iterative orthogonal projections of nonlinear mappings
- IEEE Int. Symp. on Signal Processing and Information Technology (ISSPIT 2011), pp. 173-178, 2011 [doi]
-
- A. Bertoni, M. Frasca, G. Grossi, G. Valentini
- Learning functional linkage networks with a cost-sensitive approach
- Proceedings of the 20th Italian Workshop on Neural Nets (WIRN 2010), pp. 52-61, 2010 [doi]
-
- G. Grossi, F. Pedersini
- Hub-betweenness analysis in delay tolerant networks inferred by real traces
- 8th International Symposium on Modeling and Optimization in Mobile, Ad-Hoc and Wireless Networks (WiOpt 2010), pp. 318-323, 2010
-
- A. Adamo, G. Grossi, F. Pedersini
- Trade-off between hops and delays in hub-based forwarding in DTNs
- Proceedings of the 3rd IFIP Wireless Days Conference 2010, pp. 1-5, 2010 [doi]
-
- A. Adamo, G. Grossi
- Random Pruning of Blockwise Stationary Mixtures for Online BSS
- Latent Variable Analysis and Signal Separation - 9th International Conference (LVA/ICA 2010), pp. 213-220, 2010 [doi]
-
- G. Grossi
- Adaptiveness in Monotone Pseudo-Boolean Optimization and Stochastic Neural Computation
- Int. J. Neural Syst. 19(4), pp. 241-252, 2009 [doi]
-
- G. Grossi, M. Marchi, E. Pontelli, A. Provetti
- Experimental Analysis of Graph-based Answer Set Computation over Parallel and Distributed Architectures
- J. Log. Comput. 19(4), pp. 697-715, 2009 [doi]
-
- G. Grossi, F. Pedersini
- FPGA implementation of a stochastic neural network for monotonic pseudo-Boolean optimization
- Neural Networks 21(6), pp. 872-879, 2008 [doi]
-
- S. Gaito, G. Grossi, F. Pedersini
- A two-level social mobility model for trace generation
- Proc. of the 9th ACM Int. Symp. on Mobile Ad Hoc Networking and Computing (MobiHoc 2008), pp. 457-458, 2008 [doi]
-
- S. Gaito, G. Grossi, F. Pedersini, P. Rossi
- Experimental validation of a 2-level social mobility model in opportunistic networks
- Wireless Days, 2008. WD '08. 1st IFIP, pp. 334-338, 2008
-
- G. Grossi, F. Pedersini
- FPGA Implementation of an Adaptive Stochastic Neural Model
- Artificial Neural Networks - {ICANN} 2007, 17th International Conference, pp. 559-568, 2007 [doi]
-
- S. Gaito, G. Grossi
- Extending Mixture Random Pruning to Nonpolynomial Contrast Functions in FastICA
- Signal Processing and Information Technology (ISSPIT 07), IEEE Int. Symp. on, pp. 334-338, 2007 [doi]
-
- G. Grossi, M. Marchi, E. Pontelli, A. Provetti
- Experiments with answer set computation over parallel and distributed architectures
- 4th International Workshop on Answer Set Programming (ASP '07), pp. 7-20, 2007
-
- S. Gaito, G. Grossi
- Speeding Up FastICA by Mixture Random Pruning
- Independent Component Analysis and Signal Separation, 7th International Conference (ICA 2007), pp. 185-192, 2007 [doi]
-
- G. Grossi, M. Marchi, R. Posenato
- Solving maximum independent set by asynchronous distributed hopfield-type neural networks
- RAIRO - Theoretical Informatics and Applications 40(2), pp. 371-388, 2006 [doi]
-
- S. Gaito, A. Greppi, G. Grossi
- Random projections for dimensionality reduction in ICA
- International Journal of Applied Science, Engineering and Technology 15, pp. 154-158, 2006
-
- G. Grossi
- A Discrete Adaptive Stochastic Neural Model for Constrained Optimization
- Artificial Neural Networks (ICANN 2006), 16th International Conference, pp. 641-650, 2006 [doi]
-
- G. Grossi, F. Pedersini
- A Stochastic Neural Model for Graph Problems: Software and Hardware Implementation
- Neural Networks and Brain (ICNNB '05). International Conference on, pp. 115-120, 2005 [doi]
-
- G. Grossi, M. Marchi
- A New Algorithm for Answer Set Computation
- Answer Set Programming, Advances in Theory and Implementation, Proceedings of the 3rd Intl. ASP'05 Workshop, 2005
-
- A. Bertoni, P. Campadelli, G. Grossi
- A Neural Algorithm for the Maximum Clique Problem: Analysis, Experiments, and Circuit Implementation
- Algorithmica 33(1), pp. 71-88, 2002 [doi]
-
- G. Grossi, R. Posenato
- A Distributed Algorithm for Max Independent Set Problem Based on Hopfield Networks
- Neural Nets, 13th Italian Workshop on Neural Nets (WIRN 2002), pp. 64-74, 2002 [doi]
-
- A. Bertoni, P. Campadelli, G. Grossi
- Solving Min Vertex Cover with Iterated Hopfield Networks
- Neural Nets, 13th Italian Workshop on Neural Nets (WIRN'01), pp. 87-95, 2001 [doi]
-
- A. Bertoni, G. Grossi, A. Provetti, V. Kreinovich, L. Tari
- The Prospect for Answer Sets Computation by a Genetic Model
- Answer Set Programming, Towards Efficient and Scalable Knowledge Representation and Reasoning, Proceedings of the 1st Intl. ASP'01 Workshop, 2001
-
- A. Bertoni, P. Campadelli, G. Grossi
- An approximation algorithm for the maximum cut problem and its experimental analysis
- Discrete Applied Mathematics 110(1), pp. 3-12, 2001 [doi]
-
- A. Bertoni, P. Campadelli, M. Carpentieri, G. Grossi
- A Genetic Model: Analysis and Application to MAXSAT
- Evolutionary Computation 8(3), pp. 291-309, 2000 [doi]
-
- A. Bertoni, P. Campadelli, G. Grossi
- An approximation algorithm for the maximum cut problem and its experimental analysis
- Algorithms and Experiments (ALEX98), pp. 137-143, 1998
-
- G. Grossi
- Sequences of Discrete Hopfield Networks for the Maximum Clique Problem
- Neural Nets, 13th Italian Workshop on Neural Nets (WIRN'97), pp. 139-146, 1997 [doi]
-
- A. Bertoni, P. Campadelli, G. Grossi
- A Discrete Neural Algorithm for the Maximum Clique Problem: Analysis and Circuit Implementation
- Proceedings of the Workshop on Algorithm Engineering (WAE'97), pp. 84-91, 1997
-
- M. Alberti, A. Bertoni, P. Campadelli, G. Grossi, R. Posenato
- A Neural Algorithm for MAX-2SAT: Performance Analysis and Circuit Implementation
- Neural Networks 10(3), pp. 555-560, 1997 [doi]
-
- A. Bertoni, P. Campadelli, M. Carpentieri, G. Grossi
- Analysis of a Genetic Model
- Proceedings of the 7th International Conference on Genetic Algorithms, pp. 121-126, 1997
-
- A. Bertoni, P. Campadelli, M. Carpentieri, G. Grossi
- A Genetic Model and the Hopfield Networks
- Artificial Neural Networks (ICANN 96), Int. Conf., pp. 463-468, 1996 [doi]
-
- M. Alberti, A. Bertoni, P. Campadelli, G. Grossi, R. Posenato
- A neural circuit for the maximum 2-satisfiability problem
- 3rd Euromicro Workshop on Parallel and Distributed Processing (PDP '95), pp. 319-323, 1995 [doi]
-
- M. Alberti, A. Bertoni, P. Campadelli, G. Grossi, R. Posenato
- A neural circuit for the maximum 2-satisfiability problem
- Parallel and Distributed Processing. Euromicro Workshop on, pp. 319-323, 1995 [doi]
